A Neural Algorithm of Artistic Style

Paper

Abstract

• 예술, 특히 그림 분야에서 인간은 이미지가 가지고 있는 ‘내용’과 ‘스타일’의 복잡한 상호작용을 구성함으로 독특한 시각적 경험을 창조하는 기술을 터득했다. 이 과정의 알고리즘적인 기초는 알려지지 않았으며 비슷한 기능을 가진 인공 시스템도 존재하지 않는다.
• 하지만 객체 탐지와 같은 시각적 인지 분야에서는 Deep Neural Network라고 불리우는 생물학적 시각 모델이 인간에 근접한 성능을 보여주고 있다. 우리는 DNN에 기반하여 높은 인식력을 보이는 예술적 이미지를 생성해내는 인공 시스템을 소개한다.
• 이 시스템은 neural 표현을 사용하면서 임의의 이미지의 내용과 스타일을 분리 및 재조합하며, 예술적 이미지의 생성을 위한 neural algorithm을 만들어낸다. 거기에 더해 인공신경망과 생물학적 시각의 놀라운 유사성에 비추어, 우리의 작업에서는 인간이 어떻게 예술적인 형상을 창조하고 인지하는지에 대해 알고리즘적으로 이해하는 길을 제시하겠다.

Text

• 이미지 처리 문제에서 가장 뛰어난 성능을 보이는 DNN은 Convolutional Neural Network(합성곱 신경망)이다. CNN은 시각적인 정보를 피드포워드 방식에서 계층적으로 처리하는 작은 컴퓨팅 유닛의 층들을 포함한다. 각각의 유닛으로 이루어진 층은 입력 이미지로부터 특징을 추출(feature extractor)하는 이미지 필터들의 집합으로 이해할 수 있다. 따라서 주어진 층의 출력은 feature map(특성 맵)이라고 불리우는, 입력 이미지의 서로 다르게 필터된 버전들로 구성된다

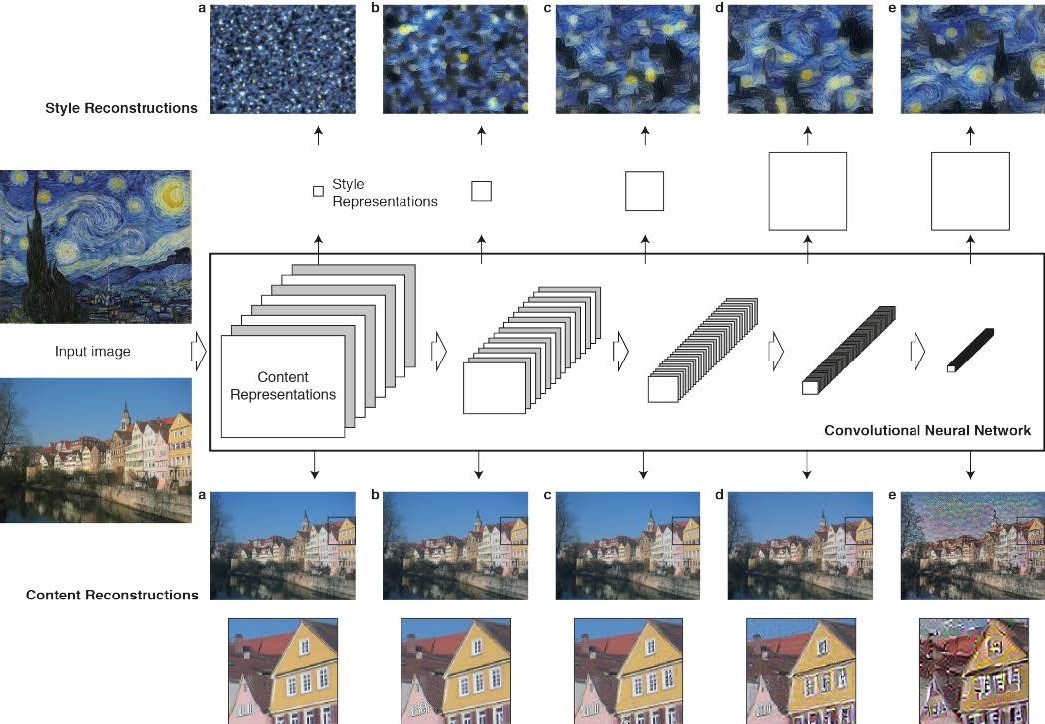
Fig 1. Convolutional Neural Network(CNN).

• CNN이 객체 인식 문제를 위해 훈련된다면, CNN은 이미지가 담고 있는 객체의 정보가 모델 내에서 처리되는 계층을 따라 점점 더 명확해지도록 발전시킨다. 따라서 신경망의 처리 계층을 따라서 입력 이미지는 구체적인 픽셀 값을 비교해서 이미지가 담고 있는 실제적인 ‘내용’을 다루는 표현으로 변환된다. 각각의 층의 특징 맵에서 이미지를 재구성함으로 우리는 입력 이미지에 대해 각각의 층이 포함하고 있는 정보를 직접적으로 시각화할 수 있다(Fig 1의 content reconstructions, Methods의 how to reconstruct the image를 확인할 것). 신경망의 높은 쪽의 층(Fig 1 content reconstructions의 d, e)은 객체와 배열의 측면에서 입력 이미지의 높은 수준의 ‘내용’ 표현을 잡아내지만 재구성의 정확한 픽셀 값을 나타내게 하지 않는다. 반면에 낮은 층의 재구성(a, b, c)은 단지 원본 이미지의 정확한 픽셀 값을 재생산할 뿐이다. 따라서 우리는 신경망의 높은 층에서의 특징 결과를 ‘content representation’으로 부른다.
• 입력 이미지의 ‘스타일’ 표현을 얻기 위해서, 우리는 텍스쳐 정보를 얻어내기 위해 설계된 feature space를 사용한다. 이 특징 공간은 신경망의 각각의 층의 filter responses 맨 위에 만들어진다. 특징 맵의 공간 범위에 대한 다양한 filter responses 사이의 상관관계를 포함한다. 다양한 층의 특징 상관관계를 포함함으로, 우리는 입력 이미지의 고정된 다중 스케일의 표현을 얻어낸다. 이 표현은 이미지의 텍스쳐 표현은 얻어내지만 그 전역적인 배열은 얻지 않는다.
• 신경망의 다양한 층에 만들어진 스타일 특성 공간에서 얻어낸 정보를 주어진 입력 이미지의 스타일 표현에 맞는 이미지를 만들어내는 방법으로 시각화할 수 있다. 스타일 특성으로부터의 재생성은 입력 이미지의 색과 국소적 구조의 관점에서의 일반화된 모습을 보여주는 텍스쳐화된 버전을 생산한다. 더욱이 이 국소적 이미지 구조의 크기와 복잡도는 계층을 따라서 증가하는데, 이는 수용 가능한 필드 크기와 특징의 복잡도의 증가로 볼 수 있다. 우리는 이러한 다중 스케일 표현을 ‘style representation’으로 부르기로 했다.

• 이 논문에서의 중요한 발견은 CNN에서의 ‘내용’과 ‘스타일’의 표현이 분리 가능하다는 것이다. 즉, 우리는 두 표현을 독립적으로 다루어 새로운, 인식적으로 의미있는 이미지를 생성해낼 수 있다. 이 발견을 입증하기 위해, 우리는 두 개의 다른 원 이미지의 내용과 스타일 표현을 섞어 이미지를 만든다. 특히, 우리는 독일 튀빙겐의 “Neckarfront” 사진의 내용 표현에, 예술의 다양한 시대에서 추린 유명한 작품들의 스타일 표현을 맞추어본다(Fig 2).

  

  Fig 2. 잘 알려진 작품들의 스타일을 합친 사진. B The Shipwreck of the Minotaur by J.M.W.Turner, 1805. C The Starry Night by Vincent van Gogh, 1889. D Der Schrei by Edvard Munch, 1893. E Femme nue assise by Pablo Picasso, 1910. F Composition VII by Wassily Kandinsky, 1913.

• 결과 이미지는 사진의 내용 표현과 각각의 예술 작품의 스타일 표현이 동시에 충족하는 이미지를 찾음으로 합성된다(Methods를 볼 것). 원 사진의 전체적인 배열은 보존이 되나, 전체적인 장면을 구성하는 색상과 국소적인 구조는 작품이 만들어낸다. 합성된 이미지가 사진의 내용은 보존하지만 그 모습이 예술 작품을 닮도록, 이 과정은 효과적으로 사진을 작품의 스타일로 렌더링한다.
• 위에서 약술한 대로, style representation은 신경망의 여러 층을 포함하는 다중 스케일의 표현이다. Fig 2에서 보인 이미지들에서, style representation은 전체 신경망 계층에서의 층들을 포함했다. 스타일은 그저 더 적은 수의 낮은 층들만을 포함함으로 더욱 국소적으로 정의될 수 있으며 이는 또 다른 시각적 경험을 보여준다(Fig 3, 행을 따라 확인). Style representation을 신경망의 높은 층으로 맞추면 국소적 이미지 구조들은 점점 더 커지는 스케일에 맞춰지며, 이는 더 부드럽고 연속적인 시각적 경험으로 이어진다. 따라서 시각적으로 가장 만족스러운 이미지들은 주로 style representation을 신경망의 최상층까지 맞추어 생성된 것들이다.

Fig 3. Wassily Kandinsky의 Composition VII의 스타일에 따른 자세한 결과물. 행은 포함되는 CNN 층을 늘림에 따른 style representation이며, 열은 내용과 스타일 재생성간의 서로 다른 가중치 비율(alpha/beta)에 따른 표현이다.

• 물론 이미지의 내용과 스타일은 완전히 분리될 수 없다. 한 이미지의 내용과 다른 이미지의 스타일을 합침으로 이미지를 생성할 때, 두 제약을 완전히 충족하는 이미지는 거의 생기지 않는다. 하지만, 이미지 합성에서 최소화하는 손실 함수는 내용과 스타일 각각 잘 분리되는 두 가지 변수를 가지고 있다(Method를 볼 것). 그래서 내용과 스타일을 재생성하는 것에 대해 중요도를 순조롭게 규제할 수 있다(Fig 3, 열을 따라 확인). 스타일에 큰 중요성을 둔다면 이미지는 작품의 모습과 일치하는 이미지를 만들어내 효과적으로 그 텍스처 버전을 제공하지만 사진의 내용을 거의 보여주지 않는다(Fig 3, 첫 번째 열). 중요성을 내용에만 둔다면 명확히 사진의 모습을 인지할 수 있으나, 그림의 스타일이 잘 확인되지 않는다(Fig 3, 마지막 열). 특정한 두 이미지에 대해서는 내용과 스타일 간의 트레이드-오프를 잘 조절하여 시각적으로 매력적인 이미지를 만들 수 있다.

Conclusion

• 이 논문에서 우리는 이미지의 내용과 스타일을 분리하여 한 이미지의 내용을 다른 이미지의 스타일에서 다시 만들어지도록 하는 인공 신경망 시스템을 소개했다. 임의로 뽑은 사진의 내용에 몇 가지 잘 알려진 그림들의 스타일이 합쳐진 새로운 예술적 이미지들을 만듦으로서 이를 입증했다. 특히, 이미지의 내용과 스타일의 neural representation을 객체 탐지에 높은 성능을 내도록 훈련된 DNN의 feature response들로부터 도출해내었다. 우리가 알기로 이 결과는 모든 자연스러운 이미지의 스타일에서 내용을 분리해내는 image feature를 처음으로 입증해내는 것이다. 스타일에서 내용을 분리하는 이전의 논문들은 훨씬 더 작은 복잡도의 입력, 이를테면 다른 필체로 쓰인 글씨 또는 작은 크기의 다른 구도를 취한 얼굴 이미지와 같은 입력에서 측정되었다.
• 우리의 입증에서, 우리는 주어진 사진을 잘 알려진 다양한 작품의 스타일로 렌더링했다. 이 문제는 주로 non-photorealistic rendering이라는 컴퓨터 비전의 한 분야의 관점에서 바라보았다. 개념상으로 가장 밀접하게 관련된 방법론은 예술적 스타일 변환을 위해 텍스처 변환을 이용하는 것이었다. 그러나 이러한 과거의 접근들은 주로 이미지의 픽셀 표현을 직접적으로 다루는 비파라미터적 기술에 기대한다. 이에 반해, 객체 탐지로 훈련된 DNN을 사용함으로 우리는 이미지가 가지고 있는 높은 수준의 내용을 명확히 표현할 수 있는 특징 공간을 조작해낼 수 있다.
• 과거에는 객체 탐지에 훈련된 DNN의 feature들은 예술 작품들이 어느 시대에 만들어졌는지를 분류하기 위한 스타일 인식을 위해 사용되어왔다. 이때 분류기는 우리가 content representation이라 부르는 신경망 활성화 함수의 맨 위에서 학습되었다. 우리는 우리의 style representation이 스타일 분류에서 더 나은 성능을 보이는 것처럼 그것을 고정된 특징 공간으로의 변환으로 추측한다.
• 일반적으로, 서로 다른 이미지에서 내용과 스타일을 섞어 새로운 이미지를 합성하는 우리의 방법은 예술, 스타일, 그리고 내용에 독립적인 이미지 외관에 대한 지각과 neural representation을 연구할 수 있는 새롭고 흥미로운 도구를 제공한다. 우리는 이미지의 모양과 내용이라는 두 가지 독립적이고 지각적으로 의미있는 변화의 원천을 도입하는 새로운 자극을 설계할 수 있다. 우리는 이것이 기능적 영상을 통한 정신물리학에서 전기생리학적 신경기록에 이르기까지 시각지각에 관한 광범위한 실험 연구에 유용할 것으로 예상한다. 사실, 우리의 결과물은 neural representation이 어떻게 이미지의 내용과 그것이 표현되는 스타일을 독립적으로 얻어내는지에 대한 알고리즘적인 이해를 제공한다. 중요한 것이은, style representation의 수학적인 식은 이미지 외관의 표현에 대해 하나의 뉴런 수준으로 내려가는 명료하고 검증 가능한 가설을 생성한다는 것이다. Style representation은 단순히 신경망의 서로 다른 종류의 뉴런들간의 상관관계를 계산한다. 뉴런들간의 상관관계를 계산하는 것은 생물학적으로 그럴듯한 계산인데, 예를 들어 primary visual system(일차 시각 피질, V1)에서의 complex cell(https://en.wikipedia.org/wiki/Complex_cell)들에 의해 만들어지는 것들과 같다. 우리의 결과는 ventral stream을 따라 서로 다른 처리 단계에서 complex-cell과 같은 계산을 수행하는 것이 시각적 입력 외관의 내용에 독립적인 표현을 얻는 방법이 될 수 있음을 제안한다.
• 생물학적 시각의 핵심 계산과제 중 하나를 수행하도록 훈련된 신경계가 이미지와 스타일을 분리할 수 있는 이미지 표현을 자동으로 학습한다는 사실은 참으로 매혹적이다. 이 사실이 객체 인식을 학습할 때 신경망은 객체의 특성을 보존하는 모든 이미지 변동에 대해 불변해야 한다는 설명이 될 수 있다. 이미지의 내용과 스타일에서의 다양성을 요인화하는 표현은 이 작업에 매우 실용적일 것이다. 따라서 스타일에서 내용을 추상화해서 예술을 창조하고 즐기는 우리의 능력은 주로 우리의 시각 시스템의 강력한 추론 능력에 따른 두드러지는 특징이 된다고 결론지을 수 있다.

Methods

• 논문에서 제시했던 결과물은 VGG 신경망(일반적인 시각적 객체 탐지 벤치마크에서 인간의 수준에 필적하는 CNN)에 기반되어 만들어졌다. 우리는 19층의 VGG 신경망의 16개의 컨볼루션 층과 5개의 풀링층이 제공하는 특성공간을 사용했다. 완전연결 층은 사용하지 않았다. 모델은 공개적으로 사용 가능하며 caffe 프레임워크로 분석이 가능하다. 이미지 합성에서 맥스풀링을 평균풀링으로 바꾸는 것이 그래이디언트 흐름을 향상시키고 더 매력적인 결과를 가져옴을 발견했으며, 따라서 위의 이미지들은 평균풀링을 이용하여 합성되었다.

• 일반적으로 신경망의 각 층은 신경망 내 층의 위치에 따라 그 복잡도가 증가하는 비선형 특성 집합을 정의한다. 따라서 주어진 입력 이미지 $\vec{x}$는 CNN의 각 층에서 이미지 필터 응답에 의해 인코딩된다. $N_l$개의 구별되는 필터를 가진 층은 특성 맵의 너비와 높이의 곱인 $M_l$를 크기로 가진 $N_l$개의 특성 맵을 가진다. 따라서 층 $l$의 응답은 행렬 $F^l \in \mathcal{R}^{N_l\times M_l}$에 저장되며 이때 $F^l_{ij}$는 층 $l$의 위치 $j$에서의 $i$번째 필터이다. 다른 단계의 층에서 인코딩되는 이미지 정보를 시각화하기 위해(Fig 1, content reconstructions) 우리는 화이트 노이즈 이미지에서 경사 하강법을 수행해 원 이미지의 특성 응답에 일치하는 또다른 이미지를 찾는다. $\vec{p}$와 $\vec{x}$를 각각 원 이미지와 생성된 이미지, 그리고 $P^l$과 $F^l$을 두 이미지의 층 $l$에서의 특성 표현이라고 하자. 그러면 두 특성 표현 사이의 squared-error loss는 다음과 같다.

  \[\begin{equation}\mathcal{L}_{content}\left(\vec{p}, \vec{x}, l\right) = \dfrac{1}{2}\sum_{i,j}\left(F^l_{ij}-P^l_{ij}\right)^2\text{ .}\end{equation}\]

  이 loss의 층 $l$에서의 activation에 대한 미분은 다음과 같다.

  \[\begin{equation}\dfrac{\partial\mathcal{L}_{content}}{\partial F^l_{ij}}=\begin{cases}\left(F^l-P^l\right)_{ij} & \text{if }F^l_{ij}>0 \\ 0 & \text{if }F^l_{ij}<0\text{ .}\end{cases}\end{equation}\]

  여기서 이미지 $\vec{x}$에 따른 그래이디언트는 표준 오차의 역전파를 이용하여 계산된다. 따라서 초기 랜덤 이미지 $\vec{x}$는 CNN의 특정 층의 응답이 원 이미지 $\vec{p}$의 응답과 같아질 때까지 바꿀 수 있다. Fig 1의 5개 content reconstructions는 원래 VGG 신경망의 ‘conv1_1’ (a), ‘conv2_1’ (b), ‘conv3_1’ (c), ‘conv4_1’ (d), ‘conv5_1’ (e)에서 이루어졌다.

• 신경망 각 층 CNN 응답의 맨 위에 서로 다른 필터 응답의 상관관계를 계산하는 style representation을 만들었으며 여기서 입력 이미지의 공간적인 확장이 기대된다.(?) 이 특성 상관관계는 Gram 행렬 $G^l \in \mathcal{R}^{N_l\times N_l}$으로부터 얻을 수 있으며, 여기서 $G_{ij}^l$은 층 $l$에서의 벡터화된 특성 맵 $i$와 $j$의 내적이다:

  \[\begin{equation}G_{ij}^l=\sum_kF_{ik}^lF_{jk}^l.\end{equation}\]

  주어진 이미지의 스타일에 맞는 질감을 생성하기 위해(Fig 1, style reconstructions), 화이트 노이즈 이미지에서 경사 하강법을 사용하여 원 이미지의 style representation에 맞는 또다른 이미지를 찾아낸다. 이는 원 이미지와 생성되는 이미지의 Gram 행렬의 entry들간의 평균 제곱 거리를 최소화함으로 이루어낸다. $\vec{a}$와 $\vec{x}$를 각각 원 이미지와 생성된 이미지, 그리고 $A^l$과 $G^l$을 두 이미지의 층 $l$에서의 style representation이라고 하자. 총 손실에 대한 층 $l$의 contribution(기여도?)은 다음과 같다.

  \[\begin{equation}E_l=\dfrac{1}{4N_l^2M_l^2}\sum_{i,j}\left(G_{ij}^l-A_{ij}^l\right)^2\end{equation}\]

  그리고 총 손실은 다음과 같다.

  \[\begin{equation}\mathcal{L}_{style}\left(\vec{a},\vec{x}\right)=\sum_{l=0}^Lw_lE_l\end{equation}\]

  여기서 $w_l$은 총 손실에 대한 각 층의 기여도의 가중치이다(아래의 결과에서 $w_l$의 구체적인 값들을 볼 수 있다). 층 $l$에서 activation에 따ㅇ른 미분 $E_l$은 다음과 같이 계산된다.

  \[\begin{equation}\dfrac{\partial E_l}{\partial F^l_{ij}}=\begin{cases}\dfrac{1}{N_l^2M_l^2}\left(\left(F^l\right)^\mathrm{T}\left(G^l-A^l\right)\right)_{ji} & \text{if }F^l_{ij}>0 \\ 0 & \text{if }F^l_{ij}<0\text{ .}\end{cases}\end{equation}\]

  신경망의 낮은 층에서의 activation에 따른 $E_l$의 그래이디언트는 표준 오차의 역전파를 이용하여 손쉽게 계산이 가능하다. Fig 1의 5 개의 style reconstruction은 층 ‘conv1_1’ (a), ‘conv1_1’과 ‘conv2_1’ (b), ‘conv1_1’, ‘conv2_1’과 ‘conv3_1’ (c), ‘conv1_1’, ‘conv2_1’, ‘conv3_1’과 ‘conv4_1’ (d), ‘conv1_1’, ‘conv2_1’, ‘conv3_1’, ‘conv4_1’과 ‘conv5_1’ (e)에서 style representaion을 맞추어 생성했다.

• 사진의 content와 그림의 style을 합성한 이미지를 생성하기 위해(Fig 2), 우리는 화이트 노이즈 이미지에서 신경망의 한 층에서 사진의 content representation과, 그리고 CNN의 다수의 층에서 그림의 style representation과의 거리를 같이 최소화한다. $\vec{p}$와 $\vec{a}$를 각각 사진과 그림이라고 하자. 우리가 최소화시킬 손실 함수는 다음과 같다.

  \[\begin{equation}\mathcal{L}_{total}\left(\vec{p},\vec{a},\vec{x}\right)=\alpha\mathcal{L}_{content}\left(\vec{p},\vec{x}\right)+\beta\mathcal{L}_{style}\left(\vec{a},\vec{x}\right)\end{equation}\]

  여기서 $\alpha$와 $\beta$는 각각 content와 style reconstruction에 대한 가중치이다. Fig 2에서 보인 이미지들을 생성하기 위해 우리는 content representation을 층 ‘conv4_2’에, style representation을 ‘conv1_1’, ‘conv_2_1’, ‘conv3_1’, ‘conv4_1’, 그리고 ‘conv_5’(다섯 층에 $w_l=1/5$, 나머지는 $w_l=0$)을 맞추었다. 비율 $\alpha/\beta$는 $1\times10^{-3}$(Fig 2의 B, C, D) 또는 $1\times10^{-4}$(Fig 2의 E, F)를 사용했다. Fig 3은 content와 style reconstruction 손실에 대한 서로 다른 가중치에 따른 결과(열을 따라)와 style representation을 ‘conv1_1’ (A), ‘conv1_1’과 ‘conv2_1’ (B), ‘conv1_1’, ‘conv2_1’과 ‘conv3_1’ (C), ‘conv1_1’, ‘conv2_1’, ‘conv3_1’과 ‘conv4_1’ (D), ‘conv1_1’, ‘conv2_1’, ‘conv3_1’, ‘conv4_1’과 ‘conv5_1’ (E)에 맞추었을 때의 결과(행을 따라)를 보여주고 있다. 가중치 $w_l$은 0이 아닌 층들에 대해 1을 항상 사용할 층들의 수로 나눈 값을 사용했다.