NIPS 2016 Tutorial: Generative Adversarial Networks

Paper

1 Why study generative modeling?

• 생성 모델을 훈련시키고 그로부터 샘플링하는 것은 고차원 확률 분포를 표현하고 다루는 능력을 확인하는 훌륭한 방법이다. 고차원 확률분포는 응용 수학 및 공학 영역의 넓은 범위에서 중요한 주제로 다루어진다.
• 모델 기반(model-based) 강화학습에 생성 모델을 포함해 학습시킬 수 있다(강화학습은 model-based와 model-free로 나뉜다). 시계열 데이터를 다루는 생성 모델은 가능한 미래를 시뮬레이션해볼 수 있다. Planning으로 쓰이는 생성 모델은 세상의 현재 상태와 에이전트의 가설에 따른 행동을 입력받아 세상의 미래 상태에 대한 조건부 분포를 학습할 수 있다. 강화학습에 쓰이는 모델에서는 잘못된 행동으로 에이전트에 해를 가하지 않도록 가상의 환경에서 학습을 할 수 있다. 또한, 특히 GAN에서는 역강화학습(inverse RL)에 쓰일 수 있다(Sec. 5.6).
• 손실 데이터와 입력에 대한 학습과 예측이 가능하다. 훈련 샘플의 대부분에 레이블이 없는 준지도학습이 특히 흥미로운 손실 데이터의 예시이다. 준지도학습의 알고리즘은 쉽게 얻을 수 있는 다량의 레이블되지 않은 샘플들을 학습함으로 일반화된다. 생성 모델, 특히 GAN이 합리적으로 준지도학습을 수행할 수 있다 (Sec 5.4).
• 머신러닝이 다중 출력을 다룰 수 있도록 한다. 많은 문제에서 하나의 입력은 다양하고 합리적인 해답과 관련이 있다. 회귀와 같은 전통적인 머신러닝 모델은 이러한 다중의 정답을 만들 수 없다.
• 많은 문제가 특정한 분포에서의 샘플의 현실적인 생성을 필요로 한다. 단일 이미지 초고해상도 생성(single image super-resolution), 예술 작품의 창조, 이미지-이미지 변환 등의 문제를 예로 들 수 있다.

2 How do generative models work? How do GANs compare to others?

2.1 Maximum likelihood estimation(최대 가능도 추정)

$\boldsymbol{\theta}$로 파라미터화되는 확률 분포를 추정하는 모델에 대해 가능도는 모델이 훈련 데이터에 할당하는 확률 $\prod_{i=1}^mp_\text{model}(\mathbf{x}^{(i)};\boldsymbol{\theta})$이다.

최대 가능도의 원리는 간단히 훈련 데이터의 가능도를 최대화하는 모델의 파라미터를 선택하는 것이다. 로그 공간에서 다루는 것이 가장 편하다(곱이 아닌 합).

\[\begin{equation}\boldsymbol{\theta}^* =\underset{\boldsymbol{\theta}}{\text{argmax}}\prod_{i=1}^mp_{\text{model}}\left(\boldsymbol{x}^{(i)};\boldsymbol{\theta}\right)\end{equation}\] \[\begin{equation}=\underset{\boldsymbol{\theta}}{\text{argmax}}\log\prod_{i=1}^mp_{\text{model}}\left(\boldsymbol{x}^{(i)};\boldsymbol{\theta}\right)\end{equation}\] \[\begin{equation}=\underset{\boldsymbol{\theta}}{\text{argmax}}\sum_{i=1}^m\log p_{\text{model}}\left(\boldsymbol{x}^{(i)};\boldsymbol{\theta}\right) .\end{equation}\]

최대 가능도 추정을 데이터 생성 분포와 모델 사이의 KL 발산 최소화로 생각할 수도 있다.

\[\begin{equation}\boldsymbol{\theta}^*=\underset{\boldsymbol{\theta}}{\text{argmin}}\ D_{\text{KL}}(p_\text{data}||p_\text{model}(\boldsymbol{x};\boldsymbol{\theta}))\ .\end{equation}\]

이 최소화를 정확하게 이뤄내고 $p_{\text{data}}$가 $p_{\text{model}}(\boldsymbol{x};\boldsymbol{\theta})$의 분포에 놓인다면 모델은 $p_{\text{data}}$를 정확하게 복원할 것이다. 실제로는 $p_{\text{data}}$에 대한 직접적인 접근없이, $p_{\text{data}}$의 m개의 샘플로 이루어진 훈련 세트을 다루게 된다. 이를 이용해 $p_{\text{data}}$를 근사하는 경험적 분포 $\hat{p}_{\text{data}}$를 정의한다.

2.2 A taxonomy of deep generative model

모든 모델이 최대 가능도를 사용한다는 가정하에 각각의 모델들을 손쉽게 비교한다. 이러한 모델들 사이에서 GAN은 각각의 모델들의 단점들을 커버하지만, 새로운 단점들도 알려지고 있다.

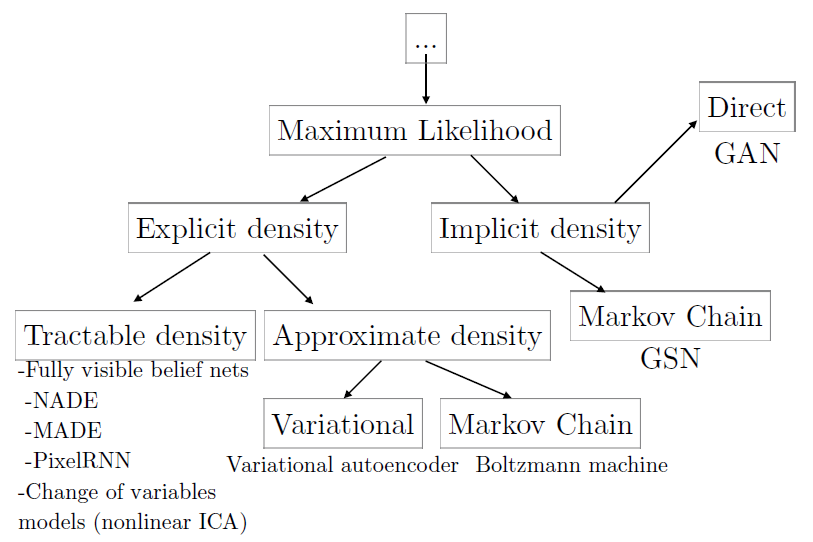
Figure 9 최대 가능도 원리를 통해 학습할 수 있는 깊은 생성 모델들은 가능도를 어떻게 표현하거나 근사하는지에 따라 구별된다.

2.3 Explicit density models $p_{\text{model}}(\boldsymbol{x};\boldsymbol{\theta})$

• 가능도 최대화 : 가능도에 대한 식에 모델 밀도 함수를 연결하여 경사 상승.
• 문제점 : 데이터의 모든 복잡성을 포함하면서 모델을 설계하는 동시에 computational tractability를 잃지 않아야 함. → tractable explicit models 그리고 explicit models requiring approximation

2.3.1 Tractable explicit models

• Fully visible belief networks(FVBNs, by Frey et al., 1996; Frey, 1998) 확률의 연쇄 규칙을 이용하여 $n$차원 벡터 $\boldsymbol{x}$의 확률 분포를 1차원 확률 분포들의 곱으로 분해하는 모델. GAN, variational autoencoder와 함께 생성 모델에서 가장 유명한 접근법이다.

  \[\begin{equation} p_\text{model}(\boldsymbol{x})=\prod_{i=1}^np_\text{model}(x_i|x_1,...,x_{i-1})\ . \end{equation}\]

  주된 단점은 샘플을 생성할 때 한 번에 한 entry $x_i$만 생성되어야 한다는 것이다(샘플 하나를 생성하는데 $O(n)$의 시간이 걸린다). WaveNet(Oord et al., 2016)과 같은 요즘의 FVBN들은 $x_i$의 확률 분포를 DNN으로 계산함으로 각각의 $n$ 스텝들은 상당한 계산이 소요된다. 그리고 이러한 과정은 병렬화되 않는다.

• Nonlinear independent components analysis 두 다른 공간 사이의 연속적인 비선형 변환 정의를 기반으로 하는 생성 모델. 잠재 변수 $\boldsymbol{z}$와 continuous, differentiable, invertible한 변환 $g$가 $\boldsymbol{x}$ 공간에서 샘플을 만들어낸다면 다음과 같다.

  \[\begin{equation} p_{x}(\boldsymbol{x})=p_z(g^{-1}(\boldsymbol{x}))\left|\ \det\left(\dfrac{\partial g^{-1}(\boldsymbol{x})}{\partial\boldsymbol{x}}\right)\right| . \end{equation}\]

  확률밀도 $p_z$와 $g^{-1}$의 야코비언의 행렬식이 tractable하면 확률밀도 $p_x$도 tractable하다. 다시 말해, 변환 $g$와 결합한 $\boldsymbol{z}$의 단순 분포는 $\boldsymbol{x}$의 복잡한 분포를 만들어낼 수 있으며 $g$가 신중하게 설계된다면 밀도 또한 tractable하다. 이러한 방식의 모델은 최소 Deco and Brauer의 논문(1995)으로 거슬러 올라가며 최근에는 real NVP (Dinh et al., 2016)가 있다.

  

  Figure 10: ImageNet의 64x64 이미지로 학습한 real NVP가 생성한 샘플들.

  주된 단점은 선택할 함수 $g$에 제한이 가해진다는 것이다. 특히 invertibility가 필요하므로 $\boldsymbol{z}$와 $\boldsymbol{x}$는 같은 차원이어야 한다.

요약: 훈련 데이터의 로그 가능도에 대해 최적화 알고리즘을 직접 사용할 수 있기 때문에 매우 효과적이나, tractable density를 제공하는 모델이 한정되어 있다.

2.3.2 Explicit models requiring approximation

• Tractable density function을 가진 모델 설계에 따른 단점을 피하기 위해, explicit density function을 사용하지만 가능도를 최대화하기 위해 근사를 사용하는 intractable한 모델들이 만들어졌다. → deterministic approximations(variational methods) 그리고 stochastic approximations(Markov chain Monte Carlo methods)

• Variational approximations(변분 근사)는 다음과 같은 하한을 정의한다.

  \[\begin{equation}\mathcal{L}(\boldsymbol{x};\boldsymbol{\theta}) \leq \log p_\text{model}(\boldsymbol{x};\boldsymbol{\theta})\ .\end{equation}\]

  $\mathcal{L}$을 최대화하는 학습 알고리즘은 적어도 $\mathcal{L}$만큼 높은 로그 가능도 값을 갖도록 보장한다. 많은 모델에서 로그 가능도가 tractable하지 않더라도 $\mathcal{L}$을 trcatable하도록 정의할 수 있다. 현재 딥러닝에서 가장 유명한 변분 학습은 variational autoencoder (VAE, Kingma, 2013; Rezende et al., 2014)이다.

  주된 단점은 사전 분포 또는 유사한 사후 분포가 너무 weak(사전 분포와 사후 분포가 매우 다를 때)할 경우, 완벽한 최적화 알고리즘과 무한한 훈련 데이터를 가지고 있다 하더라도 $\mathcal{L}$과 실제 가능도의 차이로 인해 $p_\text{model}$이 실제 $p_\text{data}$가 아닌 다른 것을 학습할 수 있다는 것이다. 실제로는 자주 좋은 가능도를 얻을 수 있지만 저품질의 샘플을 만들어낸다고 간주한다(샘플의 품질을 정량적으로 측정하는 방법이 존재하지 않음).

  

  Figure 11: CIFAR-10 데이터셋으로 학습한 VAE가 만든 샘플.

• Markov chain approximations Markov chain 테크닉을 이용하여 복잡한 샘플을 만들어 미니배치 등에 사용하는 모델. Markov chain은 샘플 \(\boldsymbol{x}'\sim q(\boldsymbol{x}' \| \boldsymbol{x})\)을 빠르게 그려 생성하는 과정이다. \(\boldsymbol{x}\)를 transition operator \(q\)에 따라 반복적으로 업데이트하면서, Markov chain은 때때로 $\boldsymbol{x}$가 \(p_\text{model}(\boldsymbol{x})\)의 한 샘플로 수렴함을 보장한다. 하지만 이 수렴이 매우 느릴 수 있고 수렴을 확인할 명확한 방법이 없으므로 실제로는 $\boldsymbol{x}$를 수렴하기 전에 너무 일찍 사용하는 경우가 있다.

  고차원 공간에서는 Markov chain이 비효율적이다. Boltzmann machines(Fahlman et al., 1983; Ackley et al., 1985; Hinton et al., 1984; Hinton and Sejnowski, 1986)은 샘플의 학습과 생성에서 Markov chain에 의존하는 생성 모델이다. 딥러닝 르네상스에서 중요한 역할이었지만 거의 쓰이지 않고, 이는 Markov chain 테크닉이 ImageNet 생성 등의 문제로 확대되지 않기 때문으로 추측된다. 게다가 학습에 확대된다고 하더라도, 이미지 생성 과정은 다중 스텝의 Markov chain이 필요하므로 상당한 수준의 계산 비용이 든다.

  한 편, Deep Boltzmann machine같은 특정 모델들은 변분 근사와 마르코프 연쇄 근사를 둘 다 사용한다.

2.4 Implicit density models

• 특정 모델들은 명시적으로 밀도 함수를 정의할 필요 없이 학습시킬 수 있다. 대신 $p_\text{model}$과 간접적으로만 상호작용하는 방식으로 모델을 학습시킨다.
• $p_\text{model}$에서 샘플을 그려내는 특정 비명시적 모델들은 Markov chain transition operator를 정의한다. 이런 종류의 시초는 generative stochastic network(Bengio et al., 2014)이다.

2.5 Comparing GANs to other generative models

GAN은 다른 생성 모델들의 단점들을 보완하여 설계되었다.

• (FVBNs) 샘플들을 병렬적으로, 샘플 차원에 비례하지 않도록 생성할 수 있다.
• (Boltzmann machines and linear ICA) 생성 함수의 설계에 제한이 매우 적다.
• (Boltzmann machines and GSNs) Markov chain이 필요 없다.
• (VAEs) Variational bound가 필요없으며 GAN 프레임워크에서 사용가능한 특정한 모델군은 universal approximator로 알려져 있어 GAN은 이미 점근적으로 일관됨(asymptotically consistent)이 알려져 있다.
• GAN은 다른 방법론들에 비해 더 좋은 샘플들을 만들어내는 것으로 간주된다.

동시에 GAN에 새로운 단점도 있다: 학습에서 목적 함수 최적화보다 어려운 내쉬 균형을 요구한다.

3 How do GANs work?

3.1 The GAN framework

• 훈련 데이터의 분포에 해당하는 것처럼 보이는 샘플을 만드는 generator와 샘플이 실제 데이터 분포에 해당하는지(real or fake)를 식별하는 discriminator의 game으로 이루어진다. Discriminator는 종래의 지도 학습 테크닉을 사용하며 입력을 두 개의 클래스로 나누어 학습된다. Generator는 discriminator를 속이도록 학습된다.

  

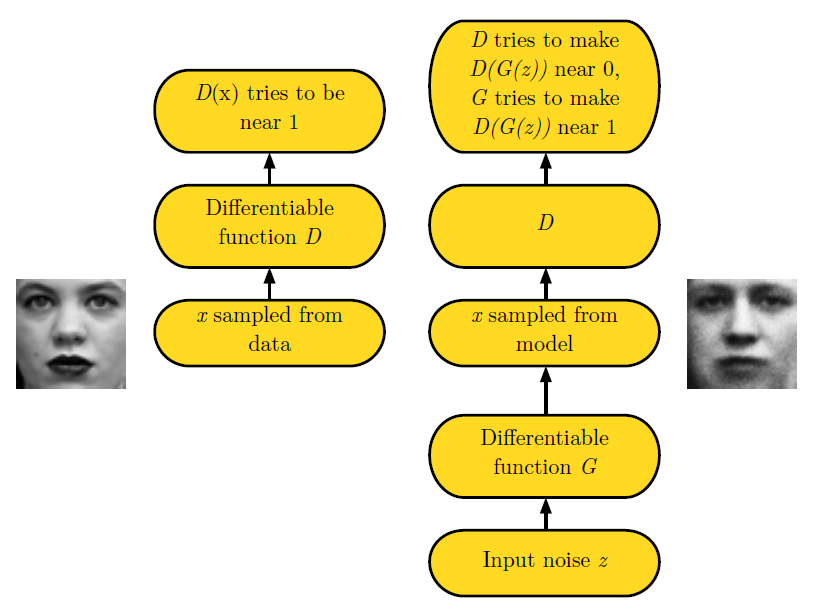
  Figure 12: GAN 프레임워크는 두 player를 경쟁시킨다. 각각의 플레이어는 파라미터 집합으로 제어되는 미분 가능한 함수로 표현된다. 일반적으로 이러한 함수들은 DNN으로 구현된다. 게임은 두 가지의 시나리오로 진행된다. 하나의 시나리오에서는 훈련 샘플 \(\boldsymbol{x}\)이 훈련 세트에서 무작위적으로 샘플링되어 함수 \(*D*\)로 표현되는 discriminator의 입력으로 사용된다. Discriminator의 목적은 입력의 절반이 실제 데이터라는 가정 하에 입력이 실제 데이터일 확률을 출력하는 것이다. 이 시나리오에서 discriminator의 목표는 \(D(\boldsymbol{x})\)를 1에 가깝게 만드는 것이다. 두 번째 시나리오에서는 generator의 입력 \(\boldsymbol{z}\)가 모델의 잠재변수에서의 사전분포에서 샘플링된다. 그 후 discriminator가 generator가 생성한 거짓 입력 \(G(\boldsymbol{z})\)를 받는다. 이 시나리오에서는 두 플레이어가 모두 참가한다. Discriminator는 \(D(G(\boldsymbol{z}))\)를 0에 가깝게, generator는 1에 가깝게 만드려 한다. 두 모델이 충분한 수준에 도달한다면 내쉬 균형이 훈련 데이터에 동일한 분포에서의 \(G(\boldsymbol{z})\)와 같으며 모든 \(\boldsymbol{x}\)에 대해 \(D(\boldsymbol{x})=\dfrac{1}{2}\)이다.

• GAN은 잠재 변수 $\boldsymbol{z}$와 관측 변수 $\boldsymbol{x}$를 포함하는 구조화된 확률 모델이다. 게임에서의 두 플레이어(생성자와 판별자)는 각각 입력과 파라미터에 대해 미분가능한 두 함수로 표현된다. 판별자는 $\boldsymbol{x}$를 입력으로 사용하는 함수 $D$로 표현하며 파라미터는 $\boldsymbol{\theta}^{(D)}$로 표현한다. 생성자는 $\boldsymbol{z}$를 입력으로 사용하는 함수 $G$로 표현하며 파라미터는 $\boldsymbol{\theta}^{(G)}$로 표현한다.

• 두 플레이어는 각각의 파라미터의 비용 함수를 가지고 있다. 판별자는 $\boldsymbol{\theta}^{(D)}$만으로 $J^{(D)}(\boldsymbol{\theta}^{(D)}, \boldsymbol{\theta}^{(G)})$를 최소화해야 하며 생성자는 $\boldsymbol{\theta}^{(G)}$만으로 $J^{(D)}(\boldsymbol{\theta}^{(D)}, \boldsymbol{\theta}^{(G)})$를 최소화해야 한다. 두 비용 함수가 상대 플레이어의 파라미터를 포함하지만 각각 상대 파라미터를 제어하지 못하므로, 이 상황을 최적화 문제가 아닌 게임으로 다룬다(즉 최솟값이 아닌 내쉬 균형이 해답이다). 여기서 우리는 local differential Nash equilibria라는 용어를 사용하겠다. 내쉬 균형은 $\boldsymbol{\theta}^{(D)}, \boldsymbol{\theta}^{(G)}$에 대해 $J^{(D)},J^{(G)}$각각 지역 최소일 때 튜플 $(\boldsymbol{\theta}^{(D)}, \boldsymbol{\theta}^{(G)})$이다.

  

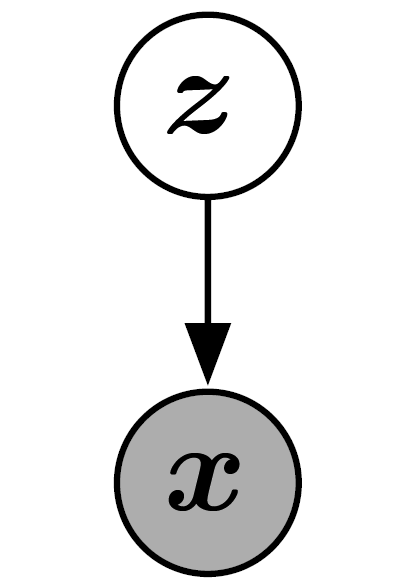
  Figure 13: GAN의 그래프 모델 구조. VAE나 sparse coding 등과 같다. 잠재변수가 모든 관측 변수에 영향을 미치는 유향 그래프 모델이다. 특정 GAN 변종들은 이러한 연결을 없애기도 한다.

• The generator 미분 가능한 함수 $G$이다. $\boldsymbol{z}$가 단순 사전 분포에서 샘플링되면 $G(\boldsymbol{z})$가 $p_\text{model}$에서 그려지는 $\boldsymbol{x}$의 샘플을 생성한다. 보통 $G$를 표현하기 위해 DNN이 쓰인다. 함수 $G$로의 입력은 DNN의 첫 번째 층에서의 입력일 필요가 없다; 입력은 신경망의 어느 부분에서도 연결될 수 있다. 예를 들어 $\boldsymbol{z}$를 $\boldsymbol{z}^{(1)}$과 $\boldsymbol{z}^{(2)}$로 나누고 $\boldsymbol{z}^{(1)}$을 신경망의 첫 번째 층에, $\boldsymbol{z}^{(2)}$를 마지막 층에 넣을 수 있다. $\boldsymbol{z}^{(2)}$가 가우시안이면 $\boldsymbol{x}$는 주어진 $\boldsymbol{z}^{(1)}$에 따라 조건적으로 가우시안이 된다. 다른 유명한 전략은 은닉층에 additive or multiplicative noise를 더하거나 noise를 연결하는 것이다.

  종합적으로 보았을 때 생성망의 설계에는 제한이 거의 없음을 알 수 있다. $p_\text{model}$이 $\boldsymbol{x}$ 공간을 완전히 표현하도록 하려면 $\boldsymbol{z}$의 차원이 $\boldsymbol{x}$의 차원만큼 커야 하고 함수 $G$가 미분 가능해야 하지만, 그것이 유일한 요구사항이다. 특히, 비선형 ICA 접근으로 학습할 수 있는 어떠한 모델도 GAN 생성망이 될 수 있다. 변분 오토인코더의 경우에는, GAN 프레임워크와 VAE 프레임워크 둘 다 학습시킬 수 있는 모델이 매우 많으나 각자 프레임워크만이 학습시킬 수 있는 모델들이 있다. 가장 두드러지는 차이는 표준 역전파에 의존할 경우 VAE는 생성기에 이산 변수를 입력으로 가질 수 없는 반면에, GAN은 출력으로 가질 수 없다는 것이다.

• The training process 학습 과정은 simultaneous SGD를 포함한다. 각각의 스텝에서 두 미니배치가 샘플링된다: 데이터셋으로부터의 $\boldsymbol{x}$값의 미니배치와 모델의 잠재변수에서의 사전분포로 그려진 $\boldsymbol{z}$의 미니배치이다. 그 후 두 그레이디언트 스텝은 동시에 이루어진다: $J^{(D)}$를 줄이기 위한 $\boldsymbol{\theta}^{(D)}$의 갱신과 $J^{(G)}$를 줄이기 위한 $\boldsymbol{\theta}^{(G)}$의 갱신이다. 두 경우에서 그레이디언트 기반 최적화를 선택할 수 있다. Adam이 보통 좋은 선택이 된다. 많은 곳에서 한 플레이어를 더 학습시키는 것을 추천하나, 저자는 각각의 플레이어에 한 스텝씩 진행하는 simultaneous gradient descent를 추천한다.

3.2 Cost functions

3.2.1 The discriminator’s cost, $J^{(D)}$

• GAN을 위해 설계된 모든 game들은 판별자에 동일한 비용 함수 $J^{(D)}$를 사용한다. 생성자에 대한 비용 함수 $J^{(G)}$만 다르다. 판별자에 대한 비용함수는 다음과 같다:

\[\begin{equation} J^{(D)}(\boldsymbol{\theta}^{(D)}, \boldsymbol{\theta}^{(G)})=-\dfrac{1}{2}\mathbb{E}_{\boldsymbol{x}\sim p_\text{data}}\log D(\boldsymbol{x})-\dfrac{1}{2}\mathbb{E}_{\boldsymbol{z}}\log (1-D(G(\boldsymbol{z}))) \ .\end{equation}\]

• 그냥 시그모이드 출력을 가진 표준 이진 분류기를 학습시킬 때 최소화되는 표준 크로스 엔트로피 비용 함수이다. 차이는 분류기가 두 미니배치에서 학습된다는 것이다; 레이블이 모두 1인 데이터셋의 미니배치와 레이블이 모두 0인 생성기의 미니배치이다.
• GAN game의 모든 종류는 판별자가 식 (8)을 최소화하도록 한다. 모든 경우에서 판별자는 똑같은 최적 전략을 가지고 있다.

• 판별자를 학습시킴으로 모든 지점 $\boldsymbol{x}$에서 다음 비율의 추정치를 계산할 수 있다:

  \[\begin{equation} \dfrac{p_\text{data}(\boldsymbol{x})}{p_\text{model}(\boldsymbol{x})} \ .\end{equation}\]

  이 비율을 추정함으로 다양한 발산과 그들의 그레이디언트를 계산할 수 있다. 이것이 GAN에 변분 오토인코더와 볼츠만 머신과의 차이를 만드는 핵심 근사 테크닉이다. 다른 깊은 생성 모델은 하한이나 마르코프 연쇄에 기반한다; GAN은 두 밀도의 비율을 추정하기 위해 지도 학습에 기반한다. GAN 근사는 지도 학습의 실패(과대와 과소적합)에 영향을 받는다. 이론적으로 완벽한 최적화와 충분한 훈련 데이터가 있으면 이러한 실패는 극복할 수 있다.

• GAN 프레임워크가 게임 이론의 도구로 자연스럽게 분석되므로 GAN을 “adversarial(적대적)”하다고 부른다. 하지만 판별자가 밀도의 비율을 추정하고 이를 생성자와 자유롭게 공유한다는 점에서 이들을 cooperative(협력적)하다고 생각할 수 있다. 이러한 관점에서 보았을 때 판별자는 생성자에게 적이기보다는 어떻게 향상할지를 지도하는 지도자에 가깝다고 볼 수 있다.

3.2.2 Minimax

• 지금까지는 판별자의 비용 함수에 대해서만 다루었다. 게임의 완전한 설명을 위해서는 생성자의 비용함수 또한 필요로 한다.

• 게임의 가장 단순한 버전은 zero-sum game이며, 여기에서는 모든 플레이어의 비용이 항상 0이다. 이 버전의 게임에서는 다음이 성립한다:

  \[\begin{equation} J^{(G)}=-J^{(D)} \ .\end{equation}\]

• $J^{(G)}$가 직접적으로 $J^{(D)}$와 연결되어 있으므로, 게임 전체를 판별자의 보상을 명시하는 가치 함수로 정리할 수 있다:

  \[\begin{equation} V\left(\boldsymbol{\theta}^{(D)}, \boldsymbol{\theta}^{(G)}\right)=-J^{(D)}\left(\boldsymbol{\theta}^{(D)}, \boldsymbol{\theta}^{(G)}\right) \ .\end{equation}\]

• 제로섬 게임은 그 해가 외부에 최소화, 내부에 최소화를 포함해 minimax 게임으로도 불린다:

  \[\begin{equation} \boldsymbol{\theta}^{(G)*}= \underset{\boldsymbol{\theta}^{(G)}}{\text{argmin}} \ \underset{\boldsymbol{\theta}^{(D)}}{\max}\ V\left(\boldsymbol{\theta}^{(D)}, \boldsymbol{\theta}^{(G)}\right) \ .\end{equation}\]
• 미니맥스 게임은 이론적 분석에 쉽게 적용이 가능해 인기가 많다. Goodfellow et al. (2014b)은 이러한 GAN 게임의 변형을 사용해, 이 게임으로 학습하는 것이 데이터와 모델 분포 간의 Jensen-Shannon 발산을 최소화하는 것과 닮았으며 두 플레이어의 정책이 함수 공간에서 직접적으로 갱신된다면 평형에 수렴한다는 것을 보였다. 실제로는 플레이어가 DNN에서 표현되고 갱신이 파라미터 공간에서 만들어지므로 이런 convexity(볼록한 정도)에 의존하는 결과는 수용되지 않는다.

3.2.3 Heuristic, non-saturating game

• 식 (10)에서 미니맥스 게임에 사용되는 생성자의 비용 함수는 이론적 분석에 유용하지만 실제로는 특별히 잘 작동하지는 않는다.
• 타깃 클래스와 분류기의 예측 분포 사이의 크로스 엔트로피를 최소화하는 것은 분류기가 틀린 출력을 보일 때는 비용이 절대 포화되지 않기 때문에 매우 효율적이다. 비용은 결국 0에 도달하며 포화되겠지만, 그 때는 오직 분류기가 올바른 클래스를 선택했을 때이다.
• 미니맥스 게임에서, 판별자는 크로스 엔트로피를 최소화하지만 생성자는 같은 크로스 엔트로피를 최대화한다. 판별자가 생성자의 샘플을 높은 신뢰도로 거부할 때 생성자의 그레이디언트가 사라지므로 생성자에게 좋지 않은 상황이다.

• 이러한 상황을 해결하기 위한 한 가지 접근으로, 생성자에게도 계속해서 크로스 엔트로피 최소화를 사용하는 것이 있다. 이 때 생성자를 위한 비용을 얻기 위해 판별자의 비용 함수의 부호를 뒤집는 대신에, 크로스 엔트로피 비용을 만들 때 사용되는 타깃을 뒤집는다. 따라서 생성자의 비용은 다음과 같다:

  \[\begin{equation} J^{(G)}=-\dfrac{1}{2}\mathbb{E}_{\boldsymbol{z}}\log D(G(\boldsymbol{z})) \ .\end{equation}\]
• 미니맥스 게임에서 생성자는 판별자가 정답을 맞출 로그 확률을 최소화 한다.
• 이 버전의 게임은 이론적이 아니라, 발견적으로 만들어졌다. 유일한 motivation은 각 플레이어가 게임에서 “패할 때” 강한 그레이디언트를 얻도록 함을 보장하는 것이었다.
• 이 버전의 게임은 더 이상 제로섬이 아니며, 하나의 가치 함수로 표현할 수 없다.

3.2.4 Maximum likelihood game

• 식 (4)와 같이, GAN으로 데이터와 모델간의 KL 발산을 최소화하는 최대 가능도 학습을 할 수 있다. Section 2에서 GAN이 다른 모델과의 비교를 단순화하기 위해 선택적으로 최대 가능도를 구현할 수 있다고 밝혔다.

• GAN 프레임워크에서 식 (4)를 근사하는 다양한 방법이 있다. Goodfellow (2014)는 식

  \[\begin{equation} J^{(G)}=-\dfrac{1}{2}\mathbb{E}_{\boldsymbol{z}}\exp\left(\sigma^{-1}( D(G(\boldsymbol{z}))) \right) \end{equation}\]

  을 사용하는 것(이 떄 $\sigma$는 로지스틱 시그모이드 함수)이 판별자가 최적이라는 가정 하에 식 (4)를 최소화하는 것과 동등함을 밝혔다. 이 동등성은 예측에서는 그대로 유지된다; 실제로는 KL 발산에서 SGD와 GAN 학습 과정은 추정된 그레이디언트를 만들기 위해 샘플링을 사용하기 때문에(최대 가능도에서는 $\boldsymbol{x}$, GAN에서는 $\boldsymbol{z}$) 실제 예상 그레이디언트에서 약간의 분산이 있을 수 있다.

3.2.5 Is the choice of divergence a distinguishing feature of GANs?

• GAN의 작동 방식에 대한 조사의 일환으로, GAN이 효과적으로 샘플을 생성하도록 하는 요소가 무엇인지를 탐구해 보겠다.
• 이전까지 VAE가 데이터와 모델간의 KL 발산을 최소화함으로 흐린 샘플을 만들어냈기에 GAN이 Jensen-Shannon 발산을 최소화함으로 뚜렷하고 현실적인 샘플을 만들어낼 것이라고 믿었다.

• KL 발산은 대칭적이지 않다; $D_{KL}(p_\text{data}||p_\text{model})$을 최소화하는 것은 $D_{KL}(p_\text{model}||p_\text{data})$를 줄이는 것과 다르다. 최대 가능도 추정은 전자를 수행하고 Jensen-Shannon 발산의 최소화는 후자에 가깝다. 그림 14에서 보여지듯이, 후자는 더 나은 샘플을 만들어내는 것으로 기대되는데 그 이유는 이러한 발산으로 훈련된 모델이 모든 모드를 포함하지만 어떠한 훈련 세트 모드에서도 비롯하지 않는 샘플을 만들어내는 것보다 일부 모드를 무시하더라도 훈련 분포의 모드에서만 샘플을 만들어내는 것을 선호하기 때문이다.

  

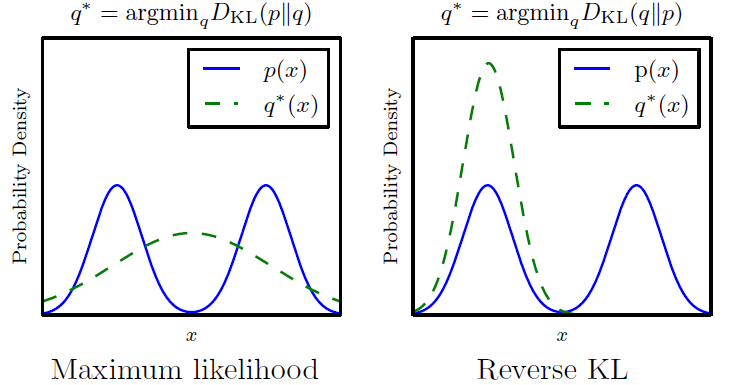
  Figure 14: KL 발산의 두 방향은 동등하지 않다. 차이는 모델의 capacity가 너무 작아 데이터 분포에 적합하지 않을 때 명확해진다. $D_{KL}(p_\text{data}||p_\text{model})$을 데이터가 존재할 모든 곳에 높은 확률을 두도록 하는 반면 $D_{KL}(p_\text{model}||p_\text{data})$은 데이터가 나타나지 않는 곳에 낮은 확률을 두도록 한다고 생각할 수 있다.

• 몇몇 새로운 증거가 Jensen-Shannon 발산의 사용이 GAN이 더 뚜렷한 샘플을 만들어내는 이유가 되지 못함을 제시하고 있다:

  • 최대 가능도를 이용해 GAN을 훈련시킬 수 있으며, 이 모델은 또한 명료한 샘플을 만들어내고 적은 수의 모드를 선택한다.

    

    Figure 15: f-GAN 모델은 많은 다양한 발산을 최소화할 수 있다. $D_{KL}(p_\text{data}||p_\text{model})$을 최소화하도록 훈련된 모델은 여전히 명확한 샘플을 만들어내고 적은 수의 모드를 선택하므로 Jensen-Shannon 발산을 선택하는 것이 GAN의 중요한 특징이 될 수 없으며 GAN의 샘플이 뚜렷한 이유가 되지 못한다고 결론지을 수 있다.

  • GAN은 자주 모델의 capacity 매우 적은 수의 모드로부터 샘플을 생성한다. Reverse KL은 일반적으로 적은 수의 모드를 선호하지 않으며 모델이 가능한 한 데이터 분포의 많은 수의 모드로부터 생성하는 것을 선호한다. 이것은 mode collapse가 발산의 선택이 아닌 다른 요소에서 기인함을 의미한다.

• 전반적으로 보았을 때, 이러한 사실은 GAN이 최소화할 발산의 선택이 아닌 훈련 단계에서의 결함으로 인하여 적은 수의 모드를 만들어냄을 제안한다. GAN이 뚜렷한 샘플을 만들어내는 이유는 명확하게 밝혀지지 않았다. GAN을 이용해 훈련된 모델군과 VAE를 이용해 훈련된 모델군의 차이에 있을 것이다(예를 들어, GAN을 사용하면 x가 단순히 생성자의 입력에 따른 등방성 가우시안 분포보다 더욱 복잡한 분포를 손쉽게 만들 수 있다). 또한 GAN이 만들어내는 근사는 다른 프레임워크가 만들어내는 것과는 다른 효과를 볼 것이다.

3.2.6 Comparison of cost functions

• 생성자 네트워크를 독특한 유형의 강화학습으로 생각할 수 있다. 생성자는 특정 출력 $\boldsymbol{x}$를 각각의 $\boldsymbol{z}$와 연결해야 한다는 메세지 없이 행동을 취하고 그에 따른 보상을 받는다. 특히 $J^{(G)}$는 훈련 데이터를 직접 참조하지 않으며, 훈련 데이터에 대한 모든 정보는 판별자가 학습한 것으로부터만 제공된다(생성자가 실제로 훈련 샘플을 직접적으로 복사할 방법이 없기 때문에 GAN은 과대적합에 내성이 있다). 훈련 과정은 과거의 강화학습과는 차이를 보이는데 그 이유는 다음과 같다:
  • 생성자가 보상 함수뿐만 아니라 그 그레이디언트까지 확인할 수 있다.
  • 보상 함수가 생성자의 정책의 변화에 따라 학습하는 판별자에 기반하므로 가변적이다.
• 모든 경우에서, 특정한 $\boldsymbol{z}$ 값을 선택함으로 시작하는 샘플링 과정을 다른 모든 $\boldsymbol{z}$ 값에 취하는 행동과 독립적으로 하나의 보상을 받는 에피소드라고 생각할 수 있다. 생성자에 주어지는 보상은 하나의 스칼라 값에 대한 함수 $D(G(\boldsymbol{z}))$이다. 주로 이 함수를 비용(음의 보상)이라고 생각한다. 생성자에 대한 비용은 함수 $D(G(\boldsymbol{z}))$에서 단조적으로 감소하지만 다른 게임들은 곡선의 다른 부분을 따라 비용을 빠르게 감소시키도록 설계된다.

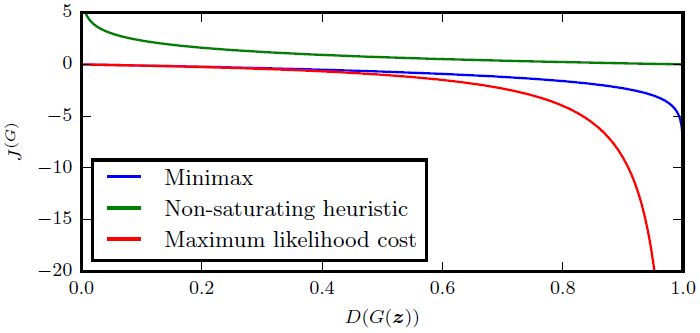
Figure 16: 생성자가 샘플 $G(\boldsymbol{z})$를 생성하면서 얻게 되는 비용은 오직 샘플에 대한 판별자의 반응에만 의존한다. 판별자가 샘플을 참이라고 할당할 확률이 커질 수록, 생성자는 더 적은 비용을 받게 된다. 샘플이 거짓이라면, 미니맥스 게임과 최대 가능도 게임은 그래프의 왼쪽 위에서 매우 적은 그레이디언트를 가진다. 휴리스틱 비포화 비용은 이 문제를 해결한다. 최대 가능도는 또한 거의 모든 그레이디언트가 곡선의 오른쪽에 존재하여 매우 적은 수의 샘플이 각 미니배치의 그레이디언트 연산을 차지하는 문제를 가진다. 이는 variance reduction 테크닉이 GAN, 특히 최대 가능도에 기반한 GAN의 성능을 높이는 중요한 연구 분야가 됨을 제시한다. Figure reproduced from Goodfellow (2014).

• 그림 16은 세 가지 다른 GAN 게임의 $D(G(\boldsymbol{z}))$의 cost response 곡선을 보여준다. 최대 가능도 게임은 매우 높은 분산을 보여주는데 대부분이 진짜에 가까운 샘플과 관련된 매우 적은 $\boldsymbol{z}$에 분포한다. 휴리스틱하게 설계된 비포화 비용은 더 적은 샘플 분산을 보이며, 이는 이 비용 함수가 실제로 더 성공적인 이유이다. 이러한 사실은 variance reduction 테크닉이 GAN, 특히 최대 가능도에 기반한 GAN의 성능을 높이는 중요한 연구 분야가 됨을 제시한다.

3.3 The DCGAN architecture

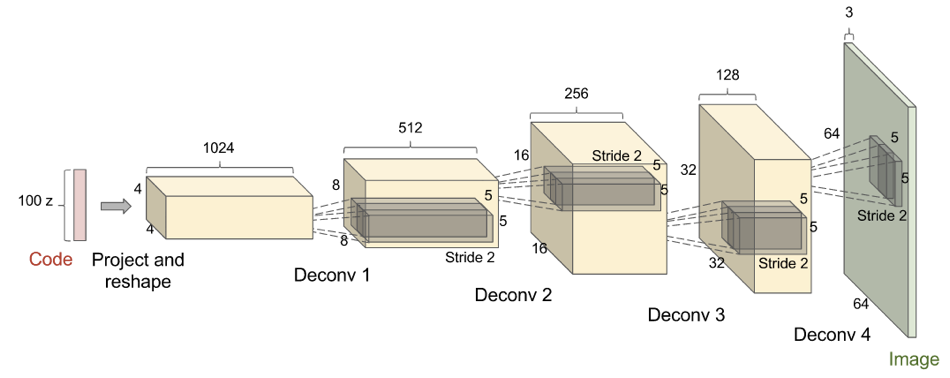
Figure 17: DCGAN에 사용된 생성자 네트워크. Figure reproduced from Radford et al. (2015).

• 오늘날의 대부분의 GAN은 어느 정도 DCGAN 구조 (Radford et al., 2015)에 기반한다. DCGAN은 “deep, convolution GAN”을 의미한다. GAN이 DCGAN 이전에도 깊고 합성곱을 사용했지만, DCGAN이라는 이름이 이러한 스타일의 구조를 의미하기에 유용하다. 이 DCGAN 구조의 핵심적인 인사이트는 다음과 같다:
  • 판별자와 생성자의 대부분의 레이어에 batch normalization(배치 정규화, Ioffe and Szegedy, 2015)를 사용했으며 , 판별자의 두 미니배치도 별도로 정규화되었다. 생성자의 마지막 레이어와 판별자의 첫 번째 레이어는 배치 정규화시키지 않음으로 모델이 데이터 분포의 정확한 평균과 크기를 학습하도록 했다.
  • 전반적인 신경망 구조는 all-convolutional net(Springenberg et al., 2015)에서 대부분을 차용했다. 이 구조는 pooling과 “unpooling” 레이어 모두 포함하지 않는다. 생성자가 공간적 차원을 확장할 필요가 있을 때 1보다 큰 stride의 전치된 컨볼루션을 수행한다.
  • 모멘텀 SGD보다는 Adam 옵티마이저를 사용한다.

• DCGAN에 앞서, LAPGAN (Denton et al., 2015)만이 고해상도 이미지로 확장할 수 있는 유일한 GAN이었다. LAPGAN은 여러 개의 GAN이 이미지의 라플라시안 피라미드 표현(참조)의 서로 다른 수준의 세부 정보를 생성하는 다단계의 생성과정을 필요로 했다. 그림 18에서 보여지듯이 DCGAN은 침실의 이미지같이 제한된 영역의 이미지에서 학습되었을 때 양질의 이미지를 생성할 수 있다. DCGAN은 또한 그림 19에서 볼 수 있듯이 잠재 공간에서의 단순 산술 연산이 입력의 semantic attribute(의미론적 특성)에 대한 산술 연산으로 명확하게 해석되는 등 GAN이 잠재 코드를 의미있게 사용함을 명료하게 입증했다.

  

  Figure 18: LSUN 데이터셋으로 학습한 DCGAN에 의해 생성된 침실 이미지 샘플.

  

  Figure 19: DCGAN은 GAN이 안경을 썻다는 개념에서 성별의 개념이 분리되는 분산 표현을 학습할 수 있음을 입증했다. 안경을 쓴 남자의 개념 표현에서 안경을 쓰지 않은 남자의 개념 표현 벡터를 빼고 안경을 쓰지 않은 여자의 개념 표현 벡터를 추가하면 안경을 쓴 여자의 개념 표현 벡터를 얻는다. 생성 모델은 이러한 표현 벡터를 올바른 분류의 이미지로 인식되도록 올바르게 해석한다. Images reproduced from Radford et al (2015).

3.4 How do GANs relate to noise-contrastive estimation and maximum likelihood?

• Noise-contrastive estimation (NCE, Gutmann and Hyvarinen, 2010)과의 연결 : 미니맥스 GAN은 NCE의 비용 함수를 가치 함수로서 사용하며, 따라서 메서드는 표면적으로 매우 관련되어 보인다. (하지만) 두 메서드가 게임에서 다른 플레이어에 주목하고 있기 때문에, 실제로는 서로 매우 다른 내용을 학습함이 밝혀졌다. 대략적으로 말해서, NCE의 목표는 판별자의 밀도 모델을 학습하는 것인 반면, GAN의 목표는 생성자를 정의하는 sampler를 학습하는 것이다. 이 두 작업이 질적인 수준에서 밀접하게 연관되어 보이지만, 그 그레이디언트는 꽤 다르다. 놀랍게도, 최대가능도가 NCE와 밀접하게 연관되었으며 같은 가치 함수를 사용하여 미니맥스 게임을 수행함이 밝혀졌다. 최대 가능도는 둘 중 하나에 경사 하강법을 사용하는 것이 아닌 휴리스틱 업데이트 전략을 사용한다.

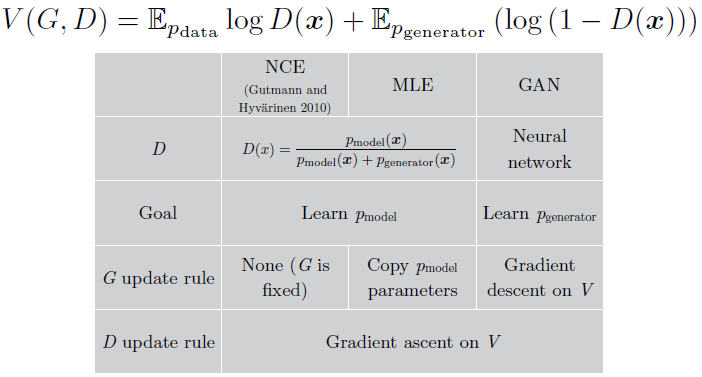
Figure 20: Goodfellow (2014)는 minimax GAN, noise-contrastive 추정, 그리고 최대 가능도가 같은 가치 함수의 미니맥스 게임 수행의 전략으로 해석될 수 있음을 설명했다. 가장 큰 차이는 $p_\text{model}$의 위치에 있다. GAN에서는 생성자가 $p_\text{model}$인 반면 NCE와 MLE에서는 $p_\text{model}$가 판별자에 속해 있다. 다른 차이는 업데이트 전략에 있다. GAN은 두 플레이어를 경사 하강법으로 학습시킨다. MLE는 판별자를 경사 하강법으로 학습시키지만, 생성자에는 휴리스틱한 업데이트 규칙을 적용시킨다. 특히, 각 판별자 업데이트 스텝 이후에 MLE는 판별자 안에서 학습된 밀도 모델을 복사하여 생성자에 쓰일 sampler로 전환한다. NCE는 생성자를 업데이트시키지 않으며 그저 노이즈의 source로서 고정되어 있다.

4 Tips and Tricks

• 이 튜토리얼에 포함되지 않은 팁과 트릭을 학습하려면 Soumith’s talk의 Github를 참고하자.

4.1 Train with labels

• 레이블을 어떠한 방식으로 사용하던지, shape나 form은 관련한 모델이 생성하는 샘플의 품질에 극적인 향상을 가져온다. 이는 Denton et al. (2015)에 의해 처음으로 관측되었다. 이후에 Salimans et al. (2016)은 생성자가 클래스의 정보를 명시적으로 포함하지 않더라도 샘플의 품질이 향상됨을 밝혔다. 즉, 판별자가 실제 객체의 특정 클래스를 인식하도록 훈련시키는 것으로 충분하다.
• 이 트릭이 어떻게 작동하는지는 전체적으로 명확하지 않다. 아마도 훈련 과정에 클래스 정보를 포함하는 것은 최적화에 유용한 단서를 제공하는 것으로 추측된다. 이 트릭은 또한 샘플의 품질에 객관적인 향상을 만들지 않고, 대신에 샘플을 인간 시각 시스템이 주목하는 특성을 취하는 방향으로 편향시킬 것이다. 만약 후자에 해당된다면 이 트릭은 실제 데이터 생성 분포에 대한 더 나은 모델에서 나아가, 대중이 즐길 수 있는 미디어 생성과 RL 에이전트가 인간과 관련된 환경과 같은 측면의 이해에 의존하는 작업을 수행하는데 도움을 줄 수 있다.
• 이 트릭을 사용함으로 얻은 결과를 같은 트릭으로 얻은 다른 결과들과만 비교하는 것이 중요하다. 레이블과 함께 학습된 모델은 레이블과 함께 학습된 모델들과 비교되어야 하며, class-conditional 모델은 다른 class-conditional 모델들과만 비교되어야 한다. 레이블을 사용하는 모델과 그렇지 않은 모델을 비교하는 것은 이미지 작업에서 컨볼루션 모델이 비 컨볼루션 모델에 비해 outperform하다는 상황만큼이나 공정하지 않으며, 흥미롭지 않은 벤치마크이다.

4.2 One-sided label smoothing

• GAN 자체는 판별자가 두 밀도의 비율을 추정할 때 작동하도록 되어있는 반면, 심층 신경망은 정확하지만 너무 극단적인 확률을 갖도록 클래스를 식별하는 높은 신뢰도의 출력을 생성하기 쉽다. 이는 특히 심층 신경망의 입력이 적대적으로 구성되는 경우에 해당된다. 이때 분류기는 선형적으로 추론하고 극단적인 신뢰도의 예측을 생성하는 경향이 있다 (Goodfellow et al., 2014a).
• 판별자가 극단적인 신뢰도의 분류를 추론하는 대신 soft probability를 추정하도록 하기 위해 one-sided label smoothing 기법을 사용할 수 있다 (Salimans et al., 2016).

• 주로 수식 (8)을 사용하여 판별자를 학습시킨다. TensorFlow (Abadi et al., 2015) 코드로 다음과 같이 작성할 수 있다:

    d_on_data = discriminator_logits(data_minibatch)
    d_on_samples = discriminator_logits(samples_minibatch)
    loss = tf.nn.sigmoid_cross_entropy_with_logits(d_on_data, 1.) + \
    			 tf.nn.sigmoid_cross_entropy_with_logits(d_on_samples,0.)
  

• One-sided label smoothing의 아이디어는 실제 예시의 타깃을 1보다 조금 적은 .9와 같은 값으로 바꾸는 것이다:

    loss = tf.nn.sigmoid_cross_entropy_with_logits(d_on_data, 0.9) + \
    			 tf.nn.sigmoid_cross_entropy_with_logits(d_on_samples,0.)
  

• 이러한 대체는 판별자의 극단적인 추론을 막는다. 판별자가 특정 입력에 대해 1에 근접하는 확률에 극단적으로 큰 logit을 예측하도록 학습된다면 패널티를 받고 그 logit을 더 적은 값으로 다시 낮추도록 인도한다.

• 거짓 샘플에 대한 레이블에는 smoothing을 적용하지 않는 것이 중요하다. 실제 데이터의 타깃으로 $1-\alpha$ 를, 거짓 샘플의 타깃으로 $0+\beta$를 사용한다면 최적 판별자 함수는 다음과 같다:

  \[\begin{equation} D^*(\boldsymbol{x})=\dfrac{(1-\alpha)p_\text{data}(\boldsymbol{x})+\beta p_\text{model}(\boldsymbol{x})}{p_\text{data}(\boldsymbol{x})+p_\text{model}(\boldsymbol{x})} \end{equation}\]
• $\beta$가 0이라면, $\alpha$를 smoothing하는 것은 판별자의 최적값만 줄인다. 하지만 $\beta$가 0이 아니라면, 최적 판별자 함수의 모양 자체가 변한다. 특히 $p_\text{data}(\boldsymbol{x})$가 매우 작고 $p_\text{model}(\boldsymbol{x})$가 더 큰 영역에서는, $D^*(\boldsymbol{x})$가 $p_\text{model}(\boldsymbol{x})$의 거짓 모드 근처에서 피크를 가질 것이다. 따라서 판별자는 생성자의 옳지 않은 행동을 강화 학습할 것이다. 생성자는 데이터를 닮은 샘플을 생성해내거나 이미 생성자가 이미 만든 샘플을 닮은 샘플을 생성해낼 것이다.
• One-sided label smoothing은 1980년대에 있었던 label smoothing 기법의 간단한 변형이다. Szegedy et al. (2015)은 label smoothing이 객체 탐지를 위한 합성곱 신경망 분야에서 훌륭한 규제가 된다고 설명했다. Label smoothing이 규제로서 잘 작동하는 이유는 모델이 학습 세트에서 옳지 않은 클래스를 선택하지 않도록 할 뿐만 아니라, 올바른 클래스에 대한 신뢰도 또한 줄여주는 데에 있다. 가중치 감소와 같은 다른 규제는 상관관계가 충분히 높게 설정되어 있을 때 자주 잘못된 분류를 만들도록 한다. Warde-Farley와 Goodfellow (2016)은 label smoothing이 판별자가 생성자의 공격에 더 효과적으로 저항하도록 학습시켜 적대적 예시에 대한 취약점을 줄여줌을 보였다.

4.3 Virtual batch normalization

• DCGAN의 도입으로 인해 대부분의 GAN 구조는 배치 정규화를 포함시켰다. 배치 정규화의 주 목적은 모델을 reparameterize하여 각 특성의 평균과 분산이 특성을 추출하는데 사용되는 모든 레이어의 가중치 사이 복잡한 상호작용이 아닌, 그 특성과 관련된 하나의 평균, 분산 파라미터로 결정되도록함으로 모델의 최적화를 향상시키는 것이다. 이 reparameterization은 데이터의 미니배치에서 특성에 평균을 빼고 표준편차로 나누는 과정으로 이루어진다. 정규화 연산이 모델의 일부로 존재해, 역전파가 항상 정규화되도록 정의된 특성의 그레이디언트를 계산한다는 사실이 중요하다. 정규화가 모델의 일부로 정의되지 않고 학습 후에 반복적으로 재정규화된다면 이러한 방법은 그 효과가 매우 떨어진다.

• 배치 정규화는 매우 도움이 되는 기법이지만, GAN에서는 좋지 않은 부작용이 있다. 훈련의 각 스텝에서 통계량의 정규화를 계산하는데 다른 미니배치를 사용하는 것은 이러한 정규화 상수의 변동을 초래한다. 미니배치의 크기가 (작은 GPU 메모리에서 큰 생성 모델을 사용하는 많은 경우와 같이) 작다면 이러한 변동이 충분히 커져 입력 $\boldsymbol{z}$가 주는 영향보다 GAN에 의해 생성된 이미지에 더 큰 영향을 줄 것이다.

  

  Figure 21: 배치 정규화를 이용하여 생성자 신경망에서 생성된 두 미니배치의 16개의 샘플. 이 미니배치들은 배치 정규화를 사용할 때 발생하는 문제를 보여준다. 미니배치 특성값의 평균과 표준편차의 변동성은 미니배치 않의 각각의 이미지들에 대한 각각의 z 코드들보다 더 큰 영향을 미칠 수 있다. 이는 주황색 샘플들을 포함하는 미니배치와 녹색 샘플들을 포함하는 미니배치에서 잘 드러난다. 미니배치 안의 예시들은 서로 독립적이어야 하지만, 배치 정규화로 인해 서로 상관관계가 형성되었다.

• Salimans et al. (2016)은 이 문제를 완화시키는 기법을 소개했다. Reference batch normalization은 신경망을 두 번 작동하는 것을 포함한다. 하나는 훈련 초기에 한번 샘플링되고 다시 사용되지 않는 reference example의 미니배치에서 작동하며, 다른 하나는 현재 훈련에 사용되는 예시의 미니배치이다. 각 특성의 평균과 표준편차는 reference batch를 사용하여 계산된다. 두 배치의 특성은 계산된 통계량을 이용하여 정규화된다. reference batch normalization의 결함은 모델이 reference batch에 과대적합될 수 있다는 것이다.
• 이 문제를 좀 더 완화시키기 위하여 virtual batch normalization이 등장했다. 여기서는 각 예제의 정규화 통계량이 예제와 reference batch의 union에서 계산된다. 두 정규화 모두 미니배치를 학습하는 과정에서 모든 예시가 서로 독립적으로 처리되며, 생성자에서 생성된 (reference batch를 제외한) 모든 샘플들은 서로 독립항등분포를 이룬다는 특성을 가지고 있다.

4.4 Can one balance $G$ and $D$?

• 많은 사람들은 두 플레이어가 서로 한 플레이어가 다른 플레이어를 압도하지 못하도록 균형을 어떻게든 유지해야 한다는 직관을 가진다. 이러한 균형이 바람직하며 실현가능하더라도, 어떠한 설득력있는 방식으로 입증되지 않았다.
• 저자는 GAN이 데이터의 밀도와 모델의 밀도의 비율의 추정에 따라 작동한다고 믿고 있다. 이 비율은 판별자가 최적일 때에만 올바르게 추정되므로, 판별자가 생성자를 압도하는 것이 그럴듯한 생각이다.
• 때로는 판별자가 너무 정확해질 경우 생성자의 그레이디언트가 사라질 수 있다. 이 문제를 해결하는 올바른 방법은 판별자의 능력을 제한하는 것이 아니라, 그레이디언트가 소멸하지 않도록 게임을 파라미터화하는 것이다 (section 3.2.3).
• 때때로 판별자의 신뢰도가 너무 높아질 경우 생성자의 그레이디언트가 매우 커질 수 있다. 판별자를 정확하지 않도록 만드는 것보다, one-sided label smoothing 기법을 사용하는 것이 더 바람직하다 (section 4.2).
• 최고의 비율 추정을 위해 판별자가 항상 최적이어야 한다는 아이디어는 생성자가 하나의 스텝을 학습할 때마다 판별자가 $k>1$ 스텝을 학습하는 방안을 제시한다. 실제로, 이는 자주 명확한 향상을 이끌어내지는 않는다.
• 모델의 크기를 선택함으로 생성자와 판별자의 균형을 조절해볼 수 있다. 실제로, 판별자가 생성자보다 종종 깊고 때때로 각 층에 더 많은 필터를 가진다. 이는 아마도 판별자가 데이터와 모델의 밀도 간 비율을 정확하게 추정할 수 있는 것이 중요한 반면에 또한 모드 붕괴 문제의 결과가 될 수 있음에 있다 (현재의 훈련 방법에서 생성자가 모든 capacity를 사용하려 하지 않기 떄문에 실무자들은 아마 생성자의 크기를 키우는 데에서 큰 효과를 보지 못한다). 모드 붕괴 문제를 극복해낼 수 있다면, 생성자의 크기는 아마도 커질 것이다. 판별자의 크기가 비례해서 커질지는 명확하지 않다.

5 Reseach Frontiers

5.1 Non-convergence

• 연구자들이 해결해야 할 GAN이 마주한 가장 큰 문제는 non-convergence(비수렴)이다.
• 대부분의 깊은 모델들은 비용 함수의 낮은 값을 찾아내는 최적화 알고리즘을 사용하여 학습된다. 많은 문제가 최적화에 방해를 줌에도, 최적화 알고리즘은 대개 믿을만한 하강 과정을 만들어낸다. GAN은 두 플레이어의 게임의 평형을 찾는 것을 요구한다. 각각의 플레이어가 업데이트에서 성공적으로 경사를 내려간다고 하더라도, 한쪽의 똑같은 업데이트가 다른 쪽 플레이어를 올라가게 할 수 있다. 때때로 두 플레이어가 결국 평형에 도달하지만, 다른 상황에서는 어떠한 유용한 상태에 도착하지 못한 채로 서로의 진행을 반복적으로 취소한다. 이는 GAN에 한정되지 않는 게임의 일반적인 문제이며, 따라서 이러한 문제의 일반적인 해답은 넓은 범위에서 응용될 수 있다.
• 동시적 경사 하강법은 일부 게임에서는 수렴을 만들지만, 모든 게임이 그러한 것은 아니다. 미니맥스 GAN 게임의 경우에, Goodfellow et al. (2014b)는 동시적 경사 하강법이 업데이트가 함수 공간에서 만들어질 때 수렴함을 보였다. 실제로는, 업데이트가 파라미터 공간에서 만들어지므로 증명이 의존하는 볼록성이 적용되지 않는다. 현재 GAN 게임이 DNN의 파라미터를 업데이트하면 수렴해야 하거나 하지 않는다는 어떠한 이론적 주장이 없다.
• 실제로는, GAN은 section 8.2의 예제에서 일어나는 것과 같이 진동하는 경우가 많으며, 이는 평형에 도달하지 않고 한 종류의 샘플을 생성하는 것에서 다른 종류의 샘플을 생성하는 것으로 진행된다.
• 아마도 GAN 게임이 마주한 가장 위협적인 형태의 비수렴 문제는 mode collapse이다.

5.1.1 Mode collapse

• Mode collapse(모드 붕괴, Helvetica scenario)는 생성자가 여러 다양한 입력 $\boldsymbol{z}$값을 같은 출력에 매핑하도록 학습될 때 나타나는 문제이다. 실제로, 완전한 모드 붕괴는 부분적 모드 붕괴는 생성자가 같은 색이나 질감을 포함하는 다수의 이미지를 생성해내거나, 같은 강아지의 다른 관점을 포함하는 다수의 이미지를 생성해내는 등의 시나리오를 의미한다.

  

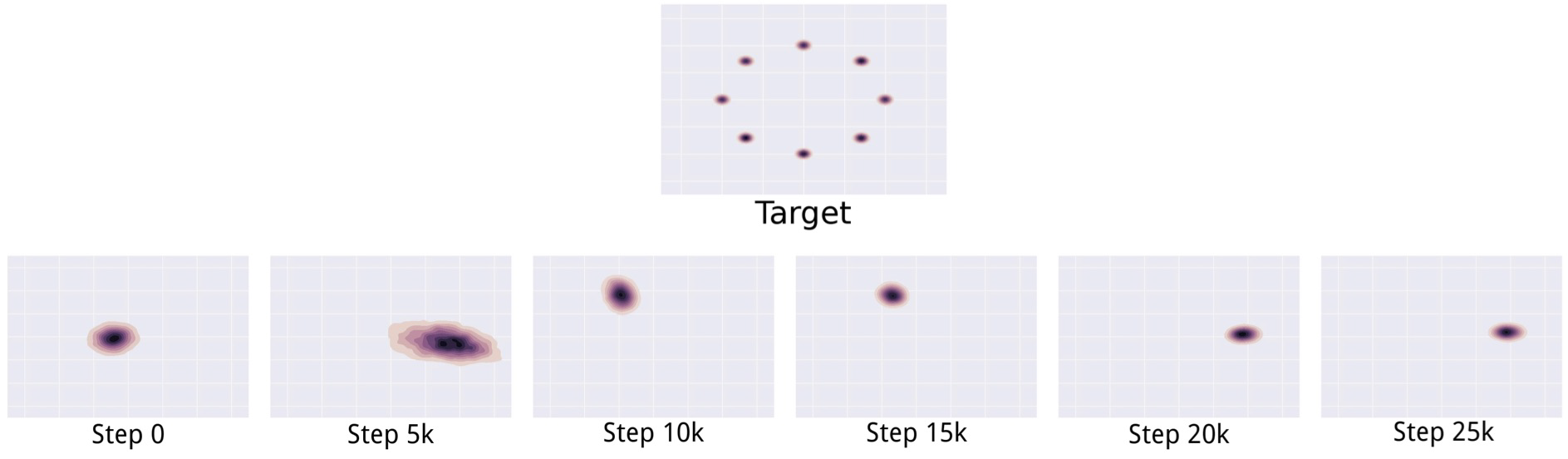
  Figure 22: 2차원 데이터셋에서의 모드 붕괴. 첫 줄에는 모델이 학습해야 할 타깃 분포 $p_\text{data}$가 있다. 그 아래에는 GAN이 시간에 따라 훈련으로 학습한 다른 분포들이 있다. 생성자는 훈련 세트의 모든 모드를 포함하는 분포로 수렴하지 않고, 그저 특정 때에 하나의 모드만을 생성해내며 그 때마다 판별자가 각각의 모드를 학습하므로 모드들 사이를 돌아다닌다. Images from Metz et al. (2016).

• 모드 붕괴는 GAN 게임의 maximin 해답의 minimax 해답으로부터의 차이에서 발생할 수 있다. 다음 모델이 있을 때:

  \[\begin{equation} G^*=\underset{G}{\min}\ \underset{D}{\max} V(G,D), \end{equation}\]

• $G^*$은 데이터 분포로부터 샘플을 그려낸다. 최소와 최대 함수의 순서를 뒤집고 다음을 찾는다면:

  \[\begin{equation} G^*=\underset{D}{\max}\ \underset{G}{\min} V(G,D), \end{equation}\]
• 생성자에 따른 최소화는 이제 최적화 과정의 내부 루프에 존재한다. 생성자는 따라서 모든 $\boldsymbol{z}$값을 판별자가 거짓이 아닌 실제라고 믿을 수 있는 하나의 $\boldsymbol{x}$좌표에 매핑하도록 유도된다. 동시적 경사 하강법은 max min에 비해 min max에 명확히 권한을 주지 않으며 반대도 마찬가지이다. 경사 하강법이 min max 처럼 행동할 것이라고 믿으며 사용하지만 max min 처럼 행동할 때도 많다.
• Section 3.2.5에서 다루었듯이, 모드 손실은 특정한 비용 함수에 의해 일어나는 것처럼 보이지는 않는다. 흔히 모드 손실이 Jensen-Shannon 발산의 사용에 의해 알어난다는 주장된다. 그러나 $D_{KL}(p_\text{data}||p_\text{model})$의 근사치를 최소화하는 GAN도 같은 문제를 겪고 있으며, 생성자가 Jensen-Shannon 발산이 선호하는 정도보다 더 적은 수의 모드들로 붕괴되는 경우가 많기 때문에 이러한 주장이 옳지 않은 것으로 보인다.

• 모드 붕괴 문제로 인하여 GAN의 적용은 종종 모델이 소수의 구별되는 출력을 만들어내는 것만이 허용되는 문제, 일반적으로 목표가 일부 입력을 많은 가능한 문제들 중 하나로 매핑하는 것이 목표가 되는 문제로 제한된다. GAN이 이러한 적은 수의 수용 가능한 출력을 찾을 수 있을지라도, GAN은 유용하다. 한 가지 예시로 text-to-image synthesis(텍스트-이미지 합성, 입력으로 이미지에 대한 설명이 주어지면 그 설명에 맞는 이미지를 출력)이 있다 (Figure 23). Reed et al. (2016a)는 GAN보다 다른 모델들이(Figure 24) 이러한 작업에서 더 다양한 출력(higher output diversity)을 보여준다는 것을 밝혔다. 하지만 StackGAN(Zhang et al. 2016)은 이전의 GAN 기반 접근법에 비해 더 다양한 출력을 보여주는 것으로 보인다(Figure 25).

  

  Figure 23: GAN을 사용한 Text-to-image synthesis. Image reproduced from Reed et al. (2016b).

  

  Figure 24: GAN은 모드 붕괴 문제로 인해 text-to-image 작업에서 낮은 출력 다양성을 보인다. Image produced from Reed et al. (2016a).

  

  Figure 25: StackGAN은 다른 GAN 기반 text-to-image 모델들보다 높은 출력 다양성을 보일 수 있다. Image reproduced from Zhang et al. (2016).

• 모드 붕괴 문제는 아마 연구자들이 해결하려고 시도해야 할 GAN의 가장 중요한 문제일 것이다. 한 가지 시도는 minibatch features (Salimans et al., 2016)이다. Minibatch feature의 기본 아이디어는 판별자가 생성된 미니배치의 example을 실제 샘플의 미니배치의 그것과 비교하도록 허용하는 것이다. 잠재 공간에서 이러한 다른 샘플의 거리를 측정함으로 판별자는 샘플이 다른 생성된 샘플들과 이상하게 비슷한지 탐지할 수 있다. Minibatch feature는 잘 작동한다. 정의에서의 작은 변화가 큰 성능 감소로 이어지므로, 이를 소개한 논문에서 공개된 Theano/TensorFlow 코드를 직접 복사해 사용할 것을 강력하게 추천한다.

• CIFAR-10 데이터셋에서 훈련된 미니배치 GAN은 대부분의 샘플이 특정 CIFAR-10 클래스로 인식되는 훌륭한 결과를 얻어냈다. 128 × 128 ImageNet 데이터셋에서 훈련되었을 때는, 소수의 이미지만이 특정 ImageNet 클래스에 속하는 것으로 인식할 수 있었다. 더 나은 이미지들을 figure 28에서 골라 놓았다.

  

  Figure 26: CIFAR-10 데이터셋에서 훈련된 미니배치 GAN은 대부분의 샘플이 특정 CIFAR-10 클래스로 인식되는 훌륭한 결과를 얻어냈다. (참고: 이 모델은 레이블을 사용하여 학습되었다)

  

  Figure 27: 128 × 128 ImageNet 데이터셋에서 훈련되었을 때는, 소수의 이미지만이 특정 ImageNet 클래스에 속하는 것으로 인식할 수 있었다.

  

  Figure 28: 미니배치 GAN은 128 × 128 ImageNet 데이터셋에서 훈련되었을 때 이 골라 놓은 예시들처럼 이따금 매우 좋은 이미지를 생성한다.

• 미니배치 GAN은 모드 붕괴 문제를 충분히 축소시켜서, 다른 counting, perspective, 그리고 global structure와 같은 문제들이 가장 명확한 결함이 되었다 (각각 figure 29, 30, 31을 참고할 것). 추측컨대 이 문제들의 많은 부분은 더 나은 모델 구조를 설계함으로 해결될 것이다.

  

  Figure 29: 128 × 128 ImageNet에서 훈련된 GAN은 빈번히 동물 신체 부분을 잘못된 수로 생성하는 등 counting에서 어려움을 겪는 것으로 보인다.

  

  Figure 30: 128 × 128 ImageNet에서 훈련된 GAN은 빈번히 너무 얇거나 이미지 축에 상당히 정렬되는 등 3D perspective의 아이디어에서 어려움을 겪는 것으로 보인다. 판별자(reader’s discriminator) 신경망의 테스트에서, 이러한 이미지 중 하나는 실제 이미지가 된다.

  

  Figure 31: 128 × 128 ImageNet에서 훈련된 GAN은 coordinating global structure에서 어려움을 겪는 것으로 보인다. 예를 들어 “Fallout Cow”라고 불리는, 네발이자 두발인 구조의 동물을 그려낸다.

• 모드 붕괴를 해결하는 다른 시도로는 unrolled GAN (Metz et al., 2016)이 있다. 이론적으로, 우리는 \(G^*=\text{arg min}_G\max_DV (G,D)\)를 찾아야 한다. 실제로는 두 플레이어의 $V(G,D)$ 그레이디언트를 동시에 따라갈 때, $G$의 그레이디언트를 계산하면서 필수적으로 max 연산을 무시하게 된다. 실제로, 우리는 $\max_DV(G,D)$를 $G$에 대한 비용 함수로 간주해야 하며, 최대화 연산 중에 역전파를 수행해야 한다. 최대화 연산에서 역전파를 수행하는 다양한 전략이 존재하지만, 음함수의 미분을 기초로 하는 다수의 전략은 불안정하다. Unrolled GAN의 아이디어는 판별자의 학습 스텝 $k$를 나타내는 계산 그래프를 만들고, 생성자의 그레이디언트를 계산할 때 모든 학습 스텝 $k$를 역전파하는 것이다. 판별자의 가치 함수를 완전히 최대화하기까지 수 만 번의 스텝이 필요하지만, Metz et al. (2016)는 10 이하로 적은 수의 스텝에 대한 unrolling으로 눈에 띄게 모드 탈락 문제를 줄일 수 있음을 밝혀냈다. 이러한 접근은 아직 ImageNet으로 확대되지는 않았다.

  

  Figure 32: Unrolled GAN은 2차원 공간 가우시안 혼합의 모든 모드들을 학습할 수 있다. Image reproduced from Metz et al. (2016).

5.1.2 Other games

• Continuous, high-dimensional non-convex game의 수렴 여부를 이해하는 방법에 대한 우리의 이론이 개선될 수 있거나, 동시적 경사 하강법보다 안정적으로 수렴하는 알고리즘을 개발해낸다면, GAN 이외의 여러 응용 분야에 도움이 될 것이다. AI 연구 분야로 한정하더라도, 많은 시나리오의 게임을 찾을 수 있다:
  • AlphaGo와 같이 (말 그대로) 게임을 하는 에이전트 (Silver et al., 2016).
  • 모델이 적대적 사례에 저항해야 하는 머신러닝 보안 (Szegedy et al., 2014; Goodfellow et al., 2014a).
  • Domain-adversarial learning을 통한 domain adaption (Ganin et al., 2015).
  • 개인정보 보존을 위한 적대적 메커니즘 (Edwards and Storkey, 2015).
  • 암호화를 위한 적대적 메커니즘 (Abadi and Andersen, 2016).

5.2 Evaluation of generative models

• GAN에서 또다른 중요한 연구 영역은 생성 모델을 양적으로 평가할 방법이 명확하지 않다는 사실에 있다. 좋은 가능도를 가지는 모델이 나쁜 샘플을 생성할 수 있고, 좋은 샘플을 생성하는 모델이 나쁜 가능도를 가질 수 있다. 샘플을 양적으로 평가할 명확하게 정의된 방법이 없다. GAN은 가능도를 추정하기가 어려워 (추정이 가능하기는 하다, Wu et al. (2016)) 다른 생성 모델보다 평가하기가 조금 더 어렵다. Theis et al. (2015)는 생성 모델을 평가하는 많은 어려움을 설명했다.

5.3 Discrete outputs

• GAN 프레임워크에서 생성자에 대한 설계에 유일한 요구 사항은 생성자가 미분가능해야 한다는 것이다. 안타깝게도 이는 생성자가 원-핫 단어 또는 글자 표현과 같은 이산 데이터를 만들어낼 수 없음을 의미한다. 이러한 한계를 없애는 것이 NLP에서 GAN의 잠재력을 해방하는 중요한 연구 방향이다. 이 문제에 접근하는 최소 세 가지 명백한 방법이 존재한다:
  1. REINFORCE(강화) 알고리즘 (Williams, 1992) 을 사용한다.
  2. Concrete distribution (Maddison et al., 2016)이나 Gumbel-softmax (Jang et al., 2016)을 사용한다.
  3. 이산 값으로 디코딩될 수 있는 연속값을 샘플링하도록 생성기를 훈련시킨다 (예를 들어 워드 임베딩을 직접 샘플링한다).

5.4 Semi-supervised learning

• GAN이 이미 매우 성공적인 연구 분야는 원래 GAN 논문 (Goodfellow et al., 2014b)에 제안되었지만 설명되지는 않은 준지도 학습에서의 생성 모델 사용이다.
• GAN은 최소 CatGAN (Springenberg, 2015)의 도입 이후에 준지도 학습에 성공적으로 적용되었다. 현재, MNIST, SVHN, 그리고 CIFAR-10에서의 준지도 학습의 state of the art(최첨단 기술)는 feature matching GAN (Salimans et al.l, 2016)에서 얻는다. 일반적으로 모델은 이러한 데이터셋에 50,000개 이상의 레이블을 사용하여 훈련되나, feature matching GAN은 매우 적은 수의 레이블을 가지고 좋은 성능을 이끌어낸다. 이 신경망은 여러 카테고리에서 20개부터 8,000개까지서로 다른 수의 레이블을 사용하여 sota 성능을 이끌어낸다.
• Feature matching GAN을 이용한 준지도 학습의 방법의 기본 아이디어는 $n$ 가지 클래스의 분류 문제를 거짓 이미지들의 하나의 클래스를 추가한 $n+1$ 가지 클래스의 분류 문제로 바꾸는 것이다. 모든 실제 클래스들은 함께 합쳐져서 이미지가 진짜일 확률을 얻는데 사용되며, 이는 GAN 게임에서 분류기를 판별자로서 사용할 수 있도록 한다. 판별기는 심지어 레이블이 없는 실제 데이터와 생성자로부터 만들어진 거짓 데이터로 학습될 수 있다. 분류기도 또한 각각의 실제 클레스를 한정된 수의 실제 레이블된 데이터로 인식하도록 훈련될 수 있다. 이러한 접근은 Salimans et al. (2016)와 Odena (2016)에 의해 동시에 개발되었다. 이전의 CatGAN에서는 $n+1$ 클래스가 아닌 $n$ 클래스 판별기를 사용했다.
• 앞으로의 GAN의 향상은 아마도 준지도 학습의 향상으로 이어질 것으로 예상된다.

5.5 Using the code

• GAN은 이미지 $\boldsymbol{x}$에 대한 표현 $\boldsymbol{z}$를 학습한다. 이 표현이 $\boldsymbol{x}$의 유용하고 고수준이며 추상적인 시멘틱 성질을 포착해낼 수 있지만, 이러한 정보를 다루는 것은 조금 어려운 일이다.
• $\boldsymbol{z}$를 사용하는데 있어 한 가지 장애물은 입력 $\boldsymbol{x}$에 대해 $\boldsymbol{z}$를 얻어내는 것이 어렵다는 것이다. Goodfellow et al. (2014b)는 생성자가 $p(\boldsymbol{x})$에서 샘플링하는 것 처럼 $p(\boldsymbol{z}|\boldsymbol{x})$로부터 샘플링하기 위한 두 번째 신경망을 사용하는 것을 제안해으나 설명하지는 않았다. 지금까지 이 아이디어의 (완전히 일반적인 신경망을 인코더로 사용하고 $p(\boldsymbol{z}|\boldsymbol{x})$의 임의의 강력한 근사치로부터 샘플링하는) 완전한 버전은 성공적으로 설명되지 않았지만, Donahue et al. (2016)은 결정론적 인코더의 훈련 방법을 설명했고, Dumoulin et al. (2016)은 사후 분포의 가우시안 근사로부터 샘플링하는 인코더 신경망의 훈련 방법을 설명했다. 추후 연구를 통해 아마도 더 강력한 확률론적 인코더를 개발할 수 있을 것이다.
• 코드를 더 잘 사용하는 또다른 방법은 코드를 더 유용하게 훈련시키는 것이다. InfoGAN (Chen et al., 2016a)에서는 $\boldsymbol{x}$와 높은 상호 상호 정보를 갖도록 하는 추가적인 목적 함수를 사용해서 코드 벡터의 일부 항목을 정규화한다. 결과 코드의 각각의 항목은 얼굴 이미지의 광원의 방향과 같은 $\boldsymbol{x}$의 특정 시멘틱 특성들과 연결된다.

5.6 Developing connections to reinforcement learning

• 연구자들은 이미 GAN과 행위자-비평가 방법론 (Pfau and Vinyals, 2016), 역강화학습 (Finn et al., 2016a) 사이의 연결을 밝혀냈으며, GAN을 모방학습 (Ho and Ermon, 2016)에 적용해냈다. 이러한 RL과의 연결은 GAN과 RL 모두에 대해 계속해서 결실을 맺어낼 것이다.

6 Plug and Play Generative Networks

• 이 튜토리얼이 NIPS에 소개되기 조금 전에, 새로운 생성 모델이 공개되었다. 이 플러그-앤-플레이 생성신경망 (Nguyen et al., 2016)은 ImageNet 클래스의 고해상도에서 생성되는 이미지 샘플들의 다양성을 극적으로 향상시켰다.
• PPGN은 새로우며 아직 잘 이해되지 않는다. 이 모델은 복잡하며, 모델 설계에 대한 대부분의 추천 사항들은 이론적 이해가 아닌 경험적 관찰에서 비롯되었다. 따라서 작동 방식은 차후에 더 명료해질 것이므로 이 튜토리얼에서 PPGN의 작동 방식을 자세하게 다루지 않을 것이다.
• 간단히 정리하자면, PPGN은 기본적으로 마르코프 체인을 사용해 이미지를 생성하기 위한 근사 Langevin 샘플링 접근이다. Langevin 샘플러의 그레이디언트는 denoising autoencoder를 사용하여 측정된다. Denoising autoencoder는 GAN 손실을 포함한 여러 손실을 이용해 학습된다.

• 일부 결과는 figure 33에서 확인할 수 있다. Figure 34에서 설명하듯이, GAN 손실은 고품질의 이미지를 얻는데 결정적으로 중요하다.

  

  Figure 33: PPGN은 ImageNet 클래스들로부터 다양한 고해상도의 이미지를 생성해낼 수 있다. Image reproduced from Nguyen et al. (2016).

  

  Figure 34: GAN 손실은 PPGN의 결정적인 요소이다. GAN 손실을 사용하지 않는다면 PPGN 구동에 사용되는 denoising autoencoder는 설득력있는 이미지를 만들어내지 못한다.

7 Exercises

8 Solutions to exercises

9 Conclusion

• GAN은 (볼츠만 머신이 마르코프 체인을 사용하는 것이나 VAE가 변분적 하한으로 근사하는 것처럼) 지도 학습을 사용하여 다루기 힘든 비용 함수를 근사하는 생성 모델이다. GAN은 지도 비율 추정 기술을 사용하여 최대 가능도 추정에 사용되는 KL 발산을 포함한 많은 비용 함수를 근사한다.
• GAN은 상대적으로 새로우며 이 새로운 잠재력에 도달하기 위해 여전히 어느 정도의 연구를 필요로 한다. 특히, GAN을 훈련시키는 것은 고차원 연속적 비볼록 게임의 내쉬 균형을 찾는 것을 필요로 한다. 연구자는 이 시나리오에 대한 더 나은 이론적 이해와 학습 알고리즘을 개발해야 한다. 이러한 방면에서의 성공은 GAN뿐만이 아닌 많은 다른 응용 분야에도 발전을 가져올 것이다.
• GAN은 많은 다양한 sota 이미지 생성과 처리 시스템에 있어 결정적인 역할을 하며, 미래에 많은 다른 응용을 가능케 할 잠재력을 가지고 있다.