U-Net: Convolutional Networks for Biomedical Image Segmentation
Abstract
깊은 신경망을 성공적으로 학습하는데 수천 개의 레이블링된 훈련 샘플이 필요하다는 사실은 모두가 동의하는 내용이다. 이 논문에서, 우리는 사용가능한 레이블링된 샘플들을 더 효율적으로 사용하기 위해 강력한 데이터 어그멘테이션에 의존하는 신경망과 훈련 전략을 소개한다. 신경망의 구조는 context를 잡아내는 수축 경로와 정밀한 localization(위치 정보 파악)을 가능케 하는 대칭되는 확장 경로(expansive path)로 구성된다. 우리는 이러한 신경망이 극소수의 이미지로 end-to-end 훈련이 가능하며 이를 통해 전자 현미경 스택에서의 신경 구조 세그멘테이션에 대한 ISBI 챌린지에서 이전의 최고 방법(sliding-window convolutional network)의 성능을 앞지름을 보여준다. 같은 신경망을 투과광 현미경 이미지(위상차와 미분간섭)에 훈련시켜, 이 카테고리에서 ISBI 2015 세포 트래킹 챌린지를 큰 폭으로 이겼다. 게다가 신경망도 빠르다. 512×512 이미지의 세그멘테이션은 최근의 GPU에서 1초도 걸리지 않는다. (Caffe에 기반한) 전체 구현과 훈련된 신경망은 http://lmb.informatik.uni-freiburg.de/people/ronneber/u-net에서 확인이 가능하다.
1 Introduction
최근 2년 동안, deep CNN은 많은 시각적 인식 작업 등에서 최신 기술로서 뛰어난 성능을 보여주고 있다. CNN은 이미 오랜 시간 존재했지만, 이 신경망의 성공은 사용가능한 훈련 세트의 크기와 관련한 신경망의 크기에 제한되었다. Krizhevsky et al.의 개선책은 8개 레이어와 1백만 개의 훈련 이미지를 가진 ImageNet에 대한 수백만 개의 파라미터로 구성된 거대한 신경망의 지도 훈련 덕분에 만들어질 수 있었다. 그 이후, 더 크고 깊은 신경망들이 훈련되었다.
CNN은 일반적으로 이미지에 대한 출력이 하나의 클래스 레이블인 분류 작업에 쓰인다. 그러나, 많은 시각적인 작업, 특히 생의학적인 이미지 처리에서 출력은 localization(클래스 레이블이 각각의 픽셀에 할당되는 것)을 포함해야 한다. 게다가, 생의학적인 작업에서 수천 개의 훈련 이미지는 보통 처리가 불가능하다. 따라서 Ciresan et al.은 슬라이딩 윈도우 구조에서 신경망을 훈련시켜 픽셀 주변의 지역 영역(패치)을 입력받아 각 픽셀의 클래스 레이블을 예측했다. 먼저, 이 신경망은 로컬라이징이 가능하다. 두 번째로, 패치라고 부르는 훈련 데이터는 훈련 이미지 수보다 훤씬 크다. 최종 네트워크는 ISBI 2012의 EM 세그멘테이션 챌린지를 큰 폭으로 우승했다.
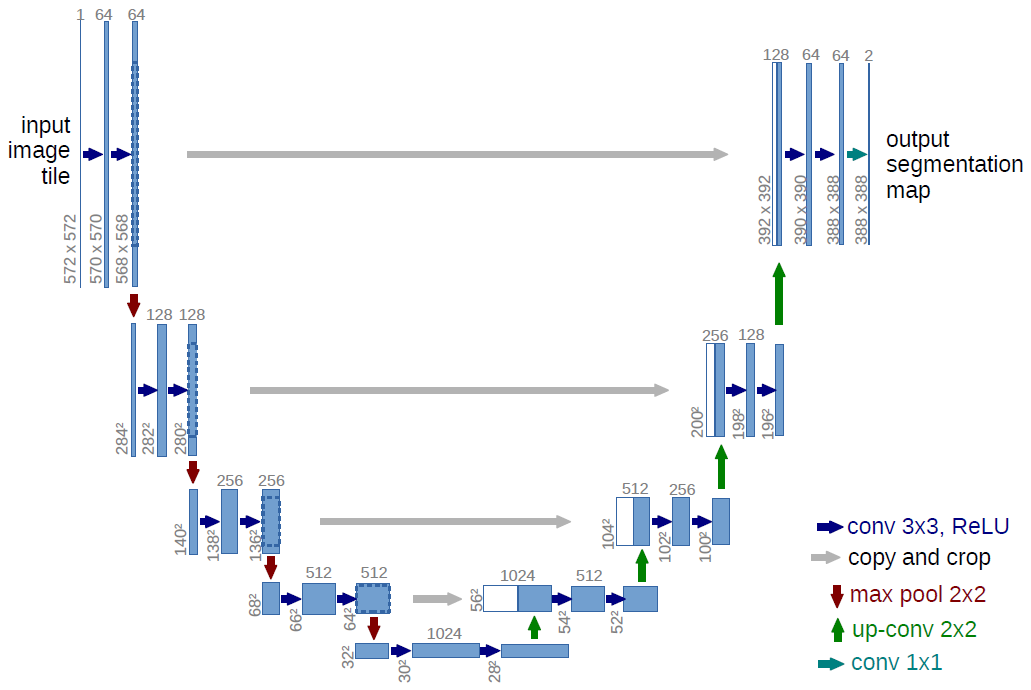
Fig. 1. U-net 구조 (최저 해상도가 32×32인 예제). 각 파랑색 박스는 다중-채널 특성 맵에 해당한다. 채널 개수는 박스 위에 적혀 있다. x-y-크기는 박스의 왼쪽 아래 모서리에 있다. 흰색 박스는 복사된 특성 맵을 표시한다. 화살표들은 서로 다른 연산을 의미한다.
명백하게, Ciresan et al.의 전략에는 두 가지 약점이 존재한다. 첫째로, 신경망이 각각의 패치에 분리되어 실행되어야 하기 때문에 꽤 느리고, 겹쳐진 패치가 존재하므로 많은 중복을 가진다. 둘째로, localization accuracy와 context간의 트레이드-오프가 존재한다. 더 큰 패치들은 더 많은 최대 풀링 레이어를 가지므로 localization accuracy가 줄어들며, 작은 패치들은 네트워크가 context만을 보도록 한다. 최근의 접근법들은 다중 레이어의 특성을 고려한 분류 출력을 제안했다. 좋은 localization과 context의 사용이 동시에 가능하다.
이 논문에서, 우리는 “fully convolutional network”라고 불리는 더 명쾌한 구조를 기반으로 삼는다. 이 구조를 수정 및 확장하여 매우 적은 수의 훈련 이미지로도 작동하고 더 정확한 세그멘테이션을 만들어내도록 한다 (Figure 1 참고). Fully convolutional network의 메인 아이디어는 일반적인 수축되는 신경망을 풀링 연산자가 업샘플링 연산자로 대체된 일련의 레이어로 보완하는 것이다. 따라서, 이 레이어들은 출력의 해상도를 키운다. Localization을 위해, 축소 경로(contracting path)에서의 고해상도의 특성들은 업샘플링된 출력과 섞인다. 그 이후 이러한 정보를 통해 일련의 컨볼루션 레이어는 더욱 정밀한 출력을 얻도록 학습된다.
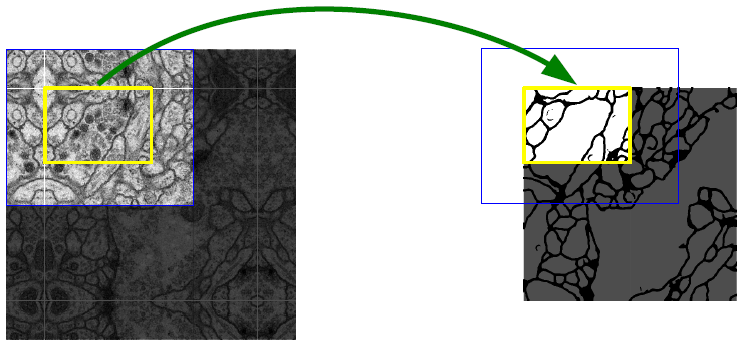
Fig. 2. 임의의 대형 이미지(여기서는 EM 스택의 신경 구조 세그멘테이션)의 원활한 세그멘테이션을 위한 overlap-tile 전략. 노랑 영역에서의 세그멘테이션 예측에 대한 입력으로 파랑 영역의 이미지 데이터를 필요로 한다. 부족한 입력 데이터는 미러링으로 외삽했다.
우리의 신경망 구조에서 한 가지 중요한 수정은 업샘플링 부분에서 거대한 크기의 특성 채널을 가지고 있어 신경망이 더 높은 해상도의 레이어에 context 정보를 전파하도록 한다는 것이다. 결과적으로, 확장 경로는 수축 경로에 비해 다소 대칭적이며, 이는 u-형태의 구조를 만들어낸다. 신경망은 완전연결층을 포함하지 않으며, 각 컨볼루션의 유효한 부분만을 사용한다. 다시 말해 세그멘테이션 맵은 입력 이미지 입력 이미지에서 전체 context를 사용할 수 있는 픽셀만 포함한다. 이러한 전략은 overlap-tile 전략을 통한 임의의 큰 이미지의 원활한 세그멘테이션을 가능케 한다 (Figure 2 참고). 이미지의 경계 영역의 픽셀들을 예측하기 위해, 부족한 context는 입력 이미지를 미러링하여 외삽한다. 이 전략 없이는 해상도가 GPU 메모리에 제한되므로, 타일링 전략은 신경망을 커다란 이미지에 적용하기에 중요하다.
우리의 작업에 사용가능한 훈련 데이터가 매우 적기 때문에, 우리는 가능한 훈련 이미지들에 elastic deformation을 적용하여 과도한 데이터 어그멘테이션을 수행한다. 이를 통해 신경망이 레이블링된 이미지 뭉치에서 변형을 확인할 필요 없이 이러한 deformation에 불변하도록 학습시킬 수 있다. 이는 특히 생의학적인 세그멘테이션에서 중요한데, 이는 deformation이 조직에서 가장 공통되는 변형이며 현실적인 deformation을 효율적으로 시뮬레이션할 수 있기 때문이다. 불변성 학습에서 데이터 어그멘테이션의 가치는 Dosovitskiy et al.에 비지도 특성 학습 범위에서 보여진다.
많은 세포 세그멘테이션 작업에서의 또다른 도전은 같은 클래스의 접촉되어 있는 객체들을 분리하는 것이다 (Figure 3 참고). 이를 위해, 우리는 접촉하는 세포들 사이의 분리 배경 레이블이 큰 가중치를 얻는 가중치 손실을 제안한다.
결과 신경망은 다양한 생의학적 세그멘테이션 문제에 적용이 가능하다. 이 논문에서 우리는 EM 스택의 신경 구조 세그멘테이션(ISBI 2012에서 비롯되어 진행중인 대회)에서 Ciresan et al.의 신경망보다 우수한 결과를 보여준다. 더 나아가, 우리는 ISBI 2015 세포 트래킹 챌린지에서 광 현미경 이미지에서 세포 세그멘테이션 결과를 보여준다. 여기에서 우리는 가장 어려운 두 가지의 2D 투과광 데이터셋에서 큰 차이로 우승했다.
2 Network Architecture
신경망의 구조는 Figure 1에 묘사되어 있다. 이 그림은 좌측에 축소 경로, 우측에 확장 경로를 포함한다. 축소 경로는 컨볼루션 신경망의 일반적인 구조를 따른다. 이는 두 3×3 (패딩이 없는) 컨볼루션과 ReLU, 그리고 다운샘플링을 위한 stride 2의 2×2 최대 풀링 레이어를 포함한다. 각 다운샘플링 단계에서 우리는 특징 채널의 수를 두 배로 늘린다. 확장 경로의 각 단계는 특징 맵의 업샘플링, 특징 채널의 수를 절반으로 줄이는 2×2 컨볼루션(“up-convolution”), 축소 경로에서 이와 관련하여 크롭한 특성 맵과의 연결, 그리고 3×3 컨볼루션과 ReLU로 구성된다. 크롭은 모든 컨볼루션의 경계 픽셀의 손실때문에 필요하다. 1×1의 마지막 레이어는 각 64-구성요소 특성 벡터를 클래스의 수에 맞추어 매핑하는데 사용된다. 최종적으로 신경망은 23개의 컨볼루션 레이어를 가진다.
출력 세그멘테이션 맵의 원활한 타일링을 위해(Figure 2를 참고), 모든 2×2 최대 풀링 연산이 x와 y의 크기가 짝수인 레이어에 적용되도록 입력 타일 크기를 설정하는 것이 중요하다.
3 Training
입력 이미지와 관련된 세그멘테이션 맵들은 Caffe에서 확률적 경사하강법으로 구현된 신경망을 훈련시키기 위해 사용된다. 패딩이 적용되지 않은 컨볼루션으로 인해, 출력 이미지는 입력 이미지에 비해 상수 크기의 테두리 너비만큼 작다. 오버헤드를 최소화하고 GPU 메모리 사용을 최대화하기 위해, 우리는 커다란 배치 크기보다 커다란 입력 타일을 선호하며 따라서 배치를 단일 이미지로 축소한다. 이에 따라 우리는 이전에 사용했던 샘플들이 현재의 최적화 스텝에서의 업데이트를 결정하도록 큰 모멘텀(0.99)를 사용한다.
에너지 함수는 크로스 엔트로피 손실 함수와 결합된 최종 특성 맵에 대해 픽셀별 소프트맥스로 계산된다. 소프트맥스는 $p_k(\mathbf{x})=\exp(a_k(\mathbf{x}))/\left(\sum_{k’=1}^K\exp(a_{k’}(\mathbf{x}))\right)$로 정의되며 이때 $a_k(\mathbf{x})$는 $\it\Omega\sub\mathbb{Z}^2$의 픽셀 위치 $\mathbf{x}\in\it\Omega$에서 특성 채널 $k$의 활성화 함수이다. $K$는 클래스의 개수이며 $p_k(\mathbf{x})$는 approximated maximum-function이다. 즉, $a_k(\mathbf{x})$가 최대인 $k$에 대해 $p_k(\mathbf{x})\approx 1$이며, 다른 모든 $k$에 대해 $p_k(\mathbf{x})\approx 0$이다. 크로스 엔트로피는 다음 식을 사용하여 $p_{\ell(\mathbf{x})}(\mathbf{x})$의 1에서의 편차에 대해 패널티를 부여한다:
\[\begin{equation} E=\sum\limits_{x\in\it\Omega}w(\mathbf{x})\log(p_{\ell(\mathbf{x})}(\mathbf{x})) \end{equation}\]여기서 $\ell : \it\Omega\rightarrow{1,…,K}$은 각 픽셀의 실제 레이블이며 $w:\it\Omega\rightarrow\mathbb{R}$은 훈련 중에 일부 픽셀에 중요성을 부여하기 위해 도입한 가중치 맵이다.

Fig. 3. DIC (differential interference contrast) 현미경으로 기록된 글라스 위의 HeLa 세포. (a) 원 이미지. (b) 실제 세그멘테이션의 오버레이. (c) 생성된 세그멘테이션 마스크 (흰색: 전경, 검은색: 배경). (d) 신경망이 경계 픽셀을 학습하도록 하는 픽셀별 손실 가중치 맵.
우리는 각각의 실제 세그멘테이션에 대한 가중치 맵을 사전학습하여 훈련 데이터 세트의 특정 클래스에서 픽셀들의 서로 다른 주파수에 대해 보상하고, 신경망이 우리가 도입한 접촉된 세포들 사이의 작은 separation border를 학습하게 하도록 한다.
Separation border는 morphological operation(모폴로지 연산, 수학적 형태학)을 사용하여 계산된다. 그 이후 가중치 맵은 다음과 같이 계산된다:
\[\begin{equation} w(\mathbf{x})=w_c(\mathbf{x})+w_0\ \cdot\ \exp\left(-\dfrac{(d_1(\mathbf{x})+d_2(\mathbf{x}))^2}{2\sigma^2}\right) \end{equation}\]여기서 $w_c:\it\Omega\rightarrow\mathbb{R}$는 클래스 주파수의 균형을 맞추기 위한 가중치 맵이며, $d_1:\it\Omega\rightarrow\mathbb{R}$는 최근접 세포와의 경계까지의 거리, 그리고 $d_2:\it\Omega\rightarrow\mathbb{R}$는 두 번째 근접 세포와의 경계까지의 거리를 의미한다. 우리의 실험에서는 $w_0=10,\sigma\approx5$로 설정했다.
많은 컨볼루션 층과 신경망을 지나는 다양한 경로로 구성된 깊은 신경망에서는, 가중치의 좋은 초기화가 극단적으로 중요하다. 초기화가 잘 되지 않을 경우 신경망의 일부는 과도한 활성화를 일으킬 수 있으며 다른 일부는 활성화가 전혀 기여하지 못할 수 있다. 이상적으로 초기 가중치들은 신경망의 각각의 특성 맵이 단위 분산에 근사하도록 적용되어야 한다. 우리의 구조가 적용된 (컨볼루션과 ReLU 층이 번갈아 나오는) 신경망에서는 이를 표준편차가 $\sqrt{2/N}$인 정규분포에서 (이 때, $N$은 한 뉴런에 들어가는 노드의 수) 초기 가중치를 설정함으로 충족이 가능하다. 예를 들어 이전 층이 3x3 컨볼루션과 64 특성 맵으로 구성되어 있다면 $N=9\ \cdot\ 64 = 576$이다.
3.1 Data Augmentation
데이터 어그멘테이션은 가능한 훈련 샘플이 매우 적을 때 신경망에 원하는 불변성(invariance)과 강건성(robustness)을 학습시키는데 필수적이다. 현미경 이미지의 경우에 우리는 주로 이동 및 회전에 대한 불변성, 그리고 변형과 회색 값 변화에 대한 강건성이 필요하다. 특히 훈련 샘플에 대한 random elastic deformation이 매우 적은 레이블링된 이미지들로 세그멘테이션 신경망을 훈련시키는데 핵심 개념이 되는 것으로 보인다. 우리는 3×3 그리드에서 무작위 변위 벡터를 사용하여 smooth deformation을 생성한다. 변위는 10 픽셀 표준편차의 정규분포에서 샘플링된다. 그 이후 픽셀당 변위는 bicubic interpolation으로 계산된다. 축소 경로의 끝에 있는 드롭아웃 층은 추가적으로 내포된 데이터 어그멘테이션을 수행한다.
4 Experiments
우리는 세 가지 다른 세그멘테이션 작업에 대한 u-net의 적용을 보여준다. 첫 번째 작업은 전자 현미경 영상에서의 신경 구조 세그멘테이션이다. 데이터 세트와 이에 대해 우리가 얻은 세그멘테이션 예시는 Figure 2에 나와 있다. 전체 결과는 Supplementary Material에 있다. 데이터 세트는 ISBI 2012에서 시작된 EM 세그멘테이션 챌린지에 있으며 새로운 기여를 위해 열려 있다. 훈련 데이터는 일련 단면 전달 전자 현미경으로 촬영한 초파리 제1령 유충의 복부 신경 코드(ventral nerve cord, VNC)의 30 장의 이미지 세트(512×512 픽셀)이다. 각 이미지에는 완전히 레이블링된 세포(흰색)와 세포막(검은색)의 실제 세그멘테이션 맵이 함께 제공된다. 테스트 세트는 사용할 수 있도록 공개되어 있지만, 세그멘테이션 맵은 비공개되어 있다. 평가는 예측된 세포막 확률 맵을 주최자에게 보내 얻을 수 있다. 이 평가는 맵을 10 가지 다른 레벨에서 임계값으로 지정하고 “warping error”, “Rand error”, 그리고 “pixel error”를 계산함으로 만들어진다.
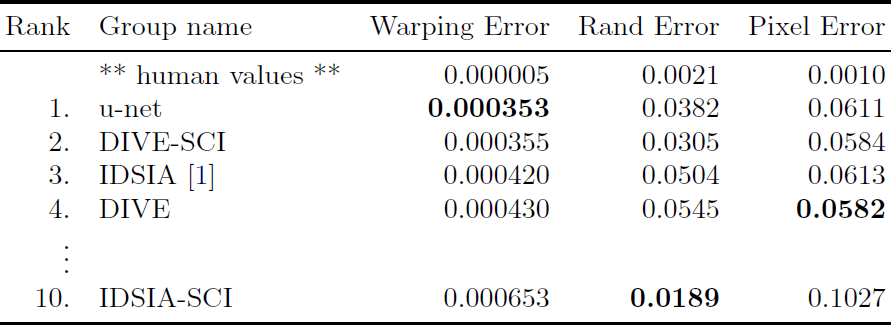
Table 1. EM 세그멘테이션 챌린지(2015년 3월 6일)의 warping error 순으로 정렬한 랭킹.
(입력 데이터의 7 가지 이상 회전된 버전을 평균내어 사용한) u-net은 어떠한 전후처리 없이 warping error 0.0003529 (새로운 최고 점수, Table 1 참조) 그리고 rand-error 0.0382를 달성했다.
이는 warping error 0.000420과 rand-error 0.0504를 보인 Ciresan el al.의 슬라이딩-윈도우 CNN보다 상당히 좋은 점수이다. Rand-error의 관점에서 보았을 때 이 데이터 세트에 대해 우리보다 좋은 성능을 보였던 유일한 알고리즘은 Ciresan et al.의 확률 맵에 적용된 상당히 데이터 세트에 특정하는 후처리 메서드를 사용했다.
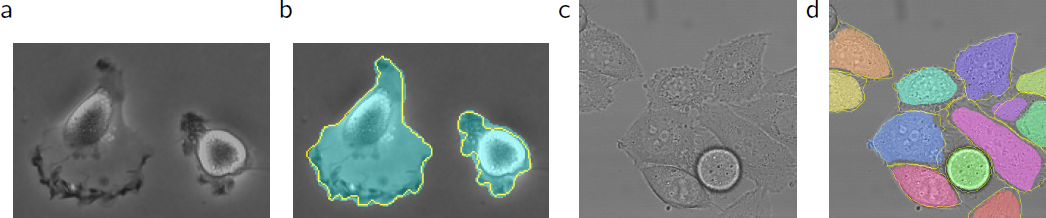
Fig. 4. ISBI 세포 트래킹 챌린지의 결과. (a) “PhC-U373” 데이터 세트의 입력 이미지 일부. (b) 수동으로 그린 실측 값(노랑 경계)과 세그멘테이션 결과(청록색 마스크) (c) “DIC-HeLa” 데이터 세트의 입력 이미지. (d) 수동으로 그린 실측 값(노랑 경계)과 세그멘테이션 결과(무작위 색 마스크).
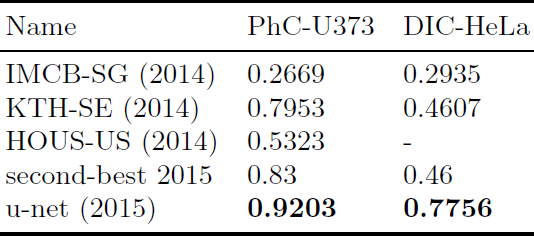
Table 2. ISBI 세포 트래킹 챌린지 2015의 세그멘테이션 결과 (IOU).
우리는 또한 u-net을 광학 현미경 이미지의 세포 세그멘테이션 작업에 적용했다. 이 세그멘테이션 작업은 ISBI 세포 트래킹 챌린지 2014와 2015의 일부이다. 첫 번째 데이터 세트 “PhC-U373”은 폴리아크릴아마이드 기질의 Glioblastoma-astrocytoma U373 세포를 위상차 현미경으로 촬영한 이미지를 담고 있다 (Figure 4a,b와 Supp. Material 참고). 이 데이터 세트는 35개의 부분적으로 레이블링된 훈련 이미지를 포함한다. 여기서 우리는 평균 IOU(“intersection over union”)으로 92%를 얻었으며 이는 83%로 두 번째로 좋은 성능을 보이는 알고리즘보다 확실히 더 좋다 (Table 2 참고). 두 번째 데이터 세트 “DIC-HeLa”는 DIC 현미경으로 촬영한 판유리 위의 HeLa 세포들이다 (Figure 3, Figure 4c,d와 Supp. Material 참고). 이 세트는 20개의 부분적으로 레이블링된 훈련 이미지들을 포함한다. 여기서 우리는 평균 IOU으로 77.5%를 얻었으며 이는 46%로 두 번째로 좋은 성능을 보이는 알고리즘보다 확실히 더 좋다.
5 Conclusion
U-net 구조는 다양한 바이오메디컬 세그멘테이션 응용에서 매우 좋은 성능을 보여준다. Elastic deformation을 이용한 데이터 어그멘테이션으로, 매우 적은 수의 레이블링된 이미지만으로 NVidia Titan GPU (6GB)에서 10시간 정도로 매우 합리적인 훈련 시간을 보여준다. Caffe 기반 구현과 훈련된 신경망을 제공한다. 우리는 u-net 구조가 더 많은 작업에 손쉽게 적용될 수 있을 것이라고 확신한다.